题目内容
设
，
为两个非零向量，则“
•
=|
•
|”是“
与
共线”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义，利用向量共线的等价条件，即可得到结论．
解答：
解：若
•
=|
•
|，
则|
|•|
|cos＜
，
＞=|
||
||cos＜
，
＞|，即cos＜
，
＞=|cos＜
，
＞|，则cos＜
，
＞≥0，则
与
共线不成立，即充分性不成立．
若
与
共线，当＜
，
＞=π，cos＜
，
＞=-1，此时
•
=|
•
|不成立，即必要性不成立，
故“
•
=|
•
|”是“
与
共线”的既不充分也不必要条件，
故选：D．
| a |
| b |
| a |
| b |
则|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故“
| a |
| b |
| a |
| b |
| a |
| b |
故选：D．
点评：本题主要考查充分条件和必要条件的应用，利用向量共线的等价条件是解决本题的关键．
练习册系列答案
相关题目
在△ABC中，∠A＜30°是cosA＞
的（ ）
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
一个空间几何体的三视图如图所示，则该几何体的体积为（ ）
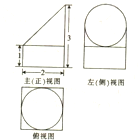
A、4+
| ||
| B、4+π | ||
| C、4+2π | ||
| D、以上都不对 |
已知F1，F2分别是双曲线C：
-
=1（a＞0，b＞0）的左、右焦点，点P在C的右支上，|PF1|，|PF2|，|F1F2|成等差数列，且∠PF1F2=120°，则该双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
在实数范围内，不等式||x-2|-1|≤1的解集为（ ）
| A、（0，4] |
| B、[0，4） |
| C、[0，4] |
| D、[1，4] |
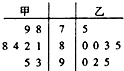甲、乙两人参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，画出茎叶图如图所示．