题目内容
已知F1,F2分别是双曲线C:
-
=1(a>0,b>0)的左、右焦点,点P在C的右支上,|PF1|,|PF2|,|F1F2|成等差数列,且∠PF1F2=120°,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:利用双曲线的定义,结合等差数列的性质,求出|PF1|、|PF2|,再利用余弦定理,建立a,c的关系,即可求出双曲线的离心率.
解答:
解:设|PF1|=m,|PF2|=n,则
∵点P在C的右支上,
∴m-n=2a,
∵|PF1|,|PF2|,|F1F2|成等差数列,
∴2n=m+2c,
∴m=4a+2c,n=2a+2c,
∵∠PF1F2=120°,
∴(4a+2c)2=(2c)2+(2a+2c)2-2•2c•(2a+2c)cos120°,
整理得3a2+ac-2c2=0,
∴2e2-e-3=0,
∵e>1,
∴e=
.
故选:A.
∵点P在C的右支上,
∴m-n=2a,
∵|PF1|,|PF2|,|F1F2|成等差数列,
∴2n=m+2c,
∴m=4a+2c,n=2a+2c,
∵∠PF1F2=120°,
∴(4a+2c)2=(2c)2+(2a+2c)2-2•2c•(2a+2c)cos120°,
整理得3a2+ac-2c2=0,
∴2e2-e-3=0,
∵e>1,
∴e=
| 3 |
| 2 |
故选:A.
点评:本题考查双曲线的性质,考查等差数列的性质,考查学生的计算能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
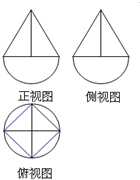 某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图由直径为2的半圆和等边三角形构成,则该几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
现有1位教师,2位男同学,3位女同学共6人站成一排,要求2位男同学站两边,3位女同学中有且仅有两位相邻,则不同排法有( )
| A、12种 | B、24种 |
| C、36种 | D、72种 |
| 2sin40°-cos10° |
| sin10° |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知f(x)=sinωx+
cosωx(ω>0)的两条相邻的对称轴间的距离为
,且f(x)图象关于点(x0,0)成中心对称,则x0可能为( )
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设
,
为两个非零向量,则“
•
=|
•
|”是“
与
共线”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某几何体的三视图如图所示,则该几何体的表面积为( )


| A、20π | B、16π |
| C、12π | D、10π |
 已知椭圆C:
已知椭圆C: