题目内容
过椭圆E:
+y2=1右焦点且垂直于x轴的直线与椭圆E相交于A,B两点,直线y=x+n与椭圆E交于C,D两点,与线段AB相交于点P(与点A和B不重合).
(Ⅰ)若AB平分CD,求CD所在直线方程.
(Ⅱ)四边形ABCD的面积是否有最大值,如果有,求出其最大面积,如果没有,请说明理由.
| x2 |
| 2 |
(Ⅰ)若AB平分CD,求CD所在直线方程.
(Ⅱ)四边形ABCD的面积是否有最大值,如果有,求出其最大面积,如果没有,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设C(x1,y1),D(x2,y2),由题意知直线AB的方程为x=1,P(
,
),由P在直线AB上,知x1+x2=2,联立
,得3x2+4nx+2n2-2=0,由此能求出CD所在的直线方程.
(Ⅱ)由已知条件推导出A(1,-
),B(1,
),P(1,1+n),-1-
<n<-1+
,四边形ACBD的面积S=
,(-1-
<n<-1+
),由函数的单调性推导出四边形ABCD的面积S没有最大值.
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
|
(Ⅱ)由已知条件推导出A(1,-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| 3-n2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:(Ⅰ)设C(x1,y1),D(x2,y2),
由题意知直线AB的方程为x=1,
∵AB平分CD,∴P为CD的中点,∴P(
,
),
∵P在直线AB上,∴x1+x2=2,
联立
,得3x2+4nx+2n2-2=0,
∴x1+x2=-
=2,解得n=-
,
∴CD所在的直线方程为y=x-
.
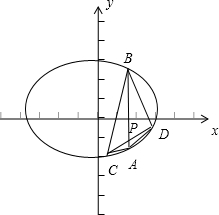 (Ⅱ)如图,∵椭圆E:
(Ⅱ)如图,∵椭圆E:
+y2=1右焦点
且垂直于x轴的直线与椭圆E相交于A,B两点,
直线y=x+n与椭圆E交于C,D两点,
与线段AB相交于点P,
∴A(1,-
),B(1,
),P(1,1+n),
∵P在AB上,∴-
<1+n<
,
解得-1-
<n<-1+
,
四边形ACBD的面积S=
•|AB|•|x2-x1|=
,
由(Ⅰ)知x1+x2=-
,x1x2=
,
代入上式,整理得S=
,(-1-
<n<-1+
),
∵在区间(-1-
,-1+
)上,S关于n单调递增,
∴四边形ABCD的面积S没有最大值.
由题意知直线AB的方程为x=1,
∵AB平分CD,∴P为CD的中点,∴P(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∵P在直线AB上,∴x1+x2=2,
联立
|
∴x1+x2=-
| 4n |
| 3 |
| 3 |
| 2 |
∴CD所在的直线方程为y=x-
| 3 |
| 2 |
 (Ⅱ)如图,∵椭圆E:
(Ⅱ)如图,∵椭圆E:| x2 |
| 2 |
且垂直于x轴的直线与椭圆E相交于A,B两点,
直线y=x+n与椭圆E交于C,D两点,
与线段AB相交于点P,
∴A(1,-
| ||
| 2 |
| ||
| 2 |
∵P在AB上,∴-
| ||
| 2 |
| ||
| 2 |
解得-1-
| ||
| 2 |
| ||
| 2 |
四边形ACBD的面积S=
| 1 |
| 2 |
| ||
| 2 |
| (x1+x2)2-4x1x2 |
由(Ⅰ)知x1+x2=-
| 4n |
| 3 |
| 2n2-2 |
| 3 |
代入上式,整理得S=
| 2 |
| 3 |
| 3-n2 |
| ||
| 2 |
| ||
| 2 |
∵在区间(-1-
| ||
| 2 |
| ||
| 2 |
∴四边形ABCD的面积S没有最大值.
点评:本题考查直线方程的求法,考查四边形面积是否有最大值的判断与求法,解题时要认真审题,注意函数的单调性的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数
在复平面内所对应的点在实轴上,那么实数a=( )
| a+i |
| 2-i |
| A、-2 | B、0 | C、1 | D、2 |
| 2sin40°-cos10° |
| sin10° |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
设
,
为两个非零向量,则“
•
=|
•
|”是“
与
共线”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某几何体的三视图如图所示,则该几何体的表面积为( )


| A、20π | B、16π |
| C、12π | D、10π |
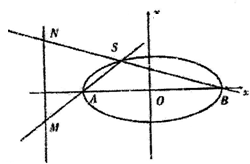 如图,已知椭圆C:
如图,已知椭圆C: 已知椭圆C:
已知椭圆C: