题目内容
在平面上，
⊥
，|
|=|
|=1，
=
+
．若|
|＜
，则|
|的取值范围是 ．
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
| OP |
| 1 |
| 3 |
| OA |
考点：向量的模
专题：平面向量及应用
分析：建立坐标系，将向量条件用等式与不等式表示，利用向量模的计算公式，即可得到结论．
解答：
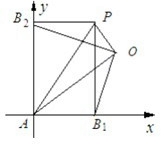
解：根据条件知A，B1，P，B2构成一个矩形AB1PB2，以AB1，AB2所在直线为坐标轴建立直角坐标系，设|AB1|=a，|AB2|=b，
点O的坐标为（x，y），则点P的坐标为（a，b），由|
|=|
|=1，得
，则
，
∵|
|＜
，
∴(x-a)2+(y-b)2＜
∴1-x2+1-y2＜
，
∴x2+y2＞
，①
∵（x-a）2+y2=1，∴y2=1-（x-a）2≤1，
∴y2≤1
同理x2≤1
∴x2+y2≤2②
由①②知
＜x2+y2≤2，
∵|
|=
，
∴
＜|
|≤
故答案为：（
，
]
点O的坐标为（x，y），则点P的坐标为（a，b），由|
| OB1 |
| OB2 |
|
|
∵|
| OP |
| 1 |
| 3 |
∴(x-a)2+(y-b)2＜
| 1 |
| 9 |
∴1-x2+1-y2＜
| 1 |
| 9 |
∴x2+y2＞
| 17 |
| 9 |
∵（x-a）2+y2=1，∴y2=1-（x-a）2≤1，
∴y2≤1
同理x2≤1
∴x2+y2≤2②
由①②知
| 17 |
| 9 |
∵|
| OA |
| x2+y2 |
∴
| ||
| 3 |
| OA |
| 2 |
故答案为：（
| ||
| 3 |
| 2 |
点评：本题考查向量知识的运用，考查学生转化问题的能力，考查学生的计算能力，属于难题
练习册系列答案
手拉手全优练考卷系列答案
相关题目
设
，
为两个非零向量，则“
•
=|
•
|”是“
与
共线”的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
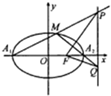如图，A1（-2，0），A2（2，0）是椭圆C：