题目内容
f（x）=
的单调减区间为 ．
| 3-2x-x2 |
考点：函数的单调性及单调区间
专题：函数的性质及应用
分析：先求函数f（x）=
的定义域，把函数f（x）=
可看作由f（x）=
和u=-x2-2x+3复合而成的，利用复合函数单调性的判断方法可求得函数的减区间．
| 3-2x-x2 |
| 3-2x-x2 |
| u |
解答：
解：f（x）=
的定义域是[-3，1]，
函数f（x）=
可看作由f（x）=
和u=-x2-2x+3复合而成的，
∵u=-x2-4x+3=-（x+1）2+7在（-∞，-2）上递增，在（-1，+∞）上递减，且f（x）=
在[-3，1]递增，
∴f（x）=
在（-∞，-1）上递增，在（-1，+∞）上递减，
∴函数f（x）=
的单调递减区间为[-1，1]，
故答案为：[-1，1]．
| 3-2x-x2 |
函数f（x）=
| 3-2x-x2 |
| u |
∵u=-x2-4x+3=-（x+1）2+7在（-∞，-2）上递增，在（-1，+∞）上递减，且f（x）=
| u |
∴f（x）=
| 3-2x-x2 |
∴函数f（x）=
| 3-2x-x2 |
故答案为：[-1，1]．
点评：本题考查复合函数单调性判断，考查幂函数、二次函数的单调性，属中档题，注意单调区间要在定义域内求解．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
设A={y|y=log2x，x＞1}，B={-2，-1，1，2}则下列结论正确的是（ ）
| A、A∩B={-2，-1} |
| B、（∁RA）∪B=（-∞，0） |
| C、A∪B=（0，+∞） |
| D、（∁RA）∩B={-2，-1} |
下列各组命题中，满足“p或q为真”，且“非p为真”的是（ ）
| A、p：0=∅；q：0∈∅ | ||||
| B、p：在△ABC中，若cos2A=cos2B，则A=B；q：y=sinx在第一象限是增函数 | ||||
C、p：a+b≥2
| ||||
D、p：圆（x-1）2+（y-2）2=1的面积被直线|x|=1平分；q：椭圆
|
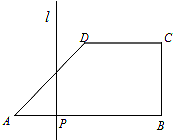在直角梯形ABCD中，AB∥DC，AB⊥BC，且AB=4，BC=CD=2，点P为线段AB上的一动点，过点P作直线l⊥AB，令AP=x，记梯形位于直线l左侧部分的面积S=f（x）．”a＜0”是”函数f（x）=|x（x-2a）|在区间（0，+∞）上单调递增”的（ ）
| A、必要不充分条件 |
| B、充要条件 |
| C、既不充分也不必要条件 |
| D、充分不必要条件 |