题目内容
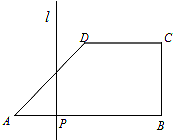 在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).
在直角梯形ABCD中,AB∥DC,AB⊥BC,且AB=4,BC=CD=2,点P为线段AB上的一动点,过点P作直线l⊥AB,令AP=x,记梯形位于直线l左侧部分的面积S=f(x).(1)求函数f(x)的解析式;
(2)作出函数f(x)的图象.
考点:分段函数的应用,函数的图象
专题:计算题,作图题,函数的性质及应用
分析:(1)过D作DE⊥AB,垂足为E,则四边形BCDE为正方形,当0≤x≤2时,梯形位于直线l左侧部分为等腰直角三角形,由三角形的面积公式即可得到;当2<x≤4时,梯形位于直线l左侧部分为等腰△ADE和矩形DEMN,由三角形的面积公式和矩形面积公式即可得到;
(2)作出分段函数的图象,注意各段的自变量的范围.
(2)作出分段函数的图象,注意各段的自变量的范围.
解答:

 解:(1)过D作DE⊥AB,垂足为E,
解:(1)过D作DE⊥AB,垂足为E,
则四边形BCDE为正方形,且AE=DE=2,
∠DAE=45°,
当0≤x≤2时,梯形位于直线l左侧部分为等腰直角三角形,则S=
x2;
当2<x≤4时,梯形位于直线l左侧部分为
等腰△ADE和矩形DEMN,
则S=
×22+2(x-2)=2x-2.
故f(x)=
;
(2)函数f(x)的图象如右图所示.

 解:(1)过D作DE⊥AB,垂足为E,
解:(1)过D作DE⊥AB,垂足为E,则四边形BCDE为正方形,且AE=DE=2,
∠DAE=45°,
当0≤x≤2时,梯形位于直线l左侧部分为等腰直角三角形,则S=
| 1 |
| 2 |
当2<x≤4时,梯形位于直线l左侧部分为
等腰△ADE和矩形DEMN,
则S=
| 1 |
| 2 |
故f(x)=
|
(2)函数f(x)的图象如右图所示.
点评:本题考查分段函数及运用,考查函数的解析式的求法和图象画法,属于中档题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知f(x)=cos 2x-1,g(x)=f(x+m)+n,则使g(x)为奇函数的实数m,n的可能取值为( )
A、m=
| ||
B、m=
| ||
C、m=-
| ||
D、m=-
|
某校高三年级有12个班,每个班随机的按1~50号排学号,为了了解某项情况,要求每班学号为20的同学去开座谈会,这里运用的是( )
| A、抽签 | B、随机数表法 |
| C、系统抽样法 | D、以上都不是 |
直线L过抛物线C:y2=2px(p>0)的焦点F且与C相交于A、B两点,且AB的中点M的坐标为(3,2),则抛物线C的方程为( )
| A、y2=2x或y2=4x |
| B、y2=4x或y2=8x |
| C、y2=6x或y2=8x |
| D、y2=2x或y2=8x |
下列结论正确的是 ( )
| A、20.2>20.1 |
| B、log34<log32 |
| C、0.3-1>0.2-1 |
| D、0.43<0.45 |
