题目内容
12.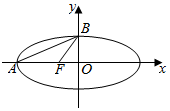 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | D. | 2 |
分析 由题意可得A(-$\sqrt{a}$,0),B(0,1),F(-$\sqrt{a-1}$,0),由∠BAO+∠BFO=90°,可得tan∠BAO•tan∠BFO=1,运用直角三角形的正切函数的定义,解方程即可得到所求a的值.
解答 解:由题意可得A(-$\sqrt{a}$,0),B(0,1),F(-$\sqrt{a-1}$,0),
由∠BAO+∠BFO=90°,可得tan∠BAO•tan∠BFO=1,
即有$\frac{BO}{AO}$•$\frac{BO}{FO}$=1,即有$\frac{1}{\sqrt{a}}$•$\frac{1}{\sqrt{a-1}}$=1,
即为a2-a-1=0,a>1,
解得a=$\frac{1+\sqrt{5}}{2}$($\frac{1-\sqrt{5}}{2}$舍去).
故选:B.
点评 本题考查椭圆的方程和性质,考查三角函数的定义的运用,以及运算能力,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
3.“a=2”是“直线2x-3y=0与直线3x+ay+1=0垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.数列{an}是递增数列,且满足an+1=f(an),a1∈(0,1),则f(x)不可能是( )
| A. | f(x)=$\sqrt{x}$ | B. | f(x)=2x-1 | C. | f(x)=$\sqrt{2x-{x}^{2}}$ | D. | f(x)=log2(x+1) |