题目内容
14．如图，在边长为2的正六边形ABCDEF中，则$\overrightarrow{AB}•\overrightarrow{CD}$=-2．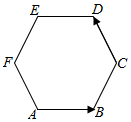
分析 根据图形，$\overrightarrow{AB}•\overrightarrow{CD}=\overrightarrow{ED}•\overrightarrow{CD}$，而$＜\overrightarrow{ED}，\overrightarrow{CD}＞=120°$，且$|\overrightarrow{ED}|=2，|\overrightarrow{CD}|=2$，这样即可求出$\overrightarrow{ED}•\overrightarrow{CD}$的值，即得出$\overrightarrow{AB}•\overrightarrow{CD}$的值．
解答 解：$\overrightarrow{AB}•\overrightarrow{CD}=\overrightarrow{ED}•\overrightarrow{CD}$=$|\overrightarrow{ED}||\overrightarrow{CD}|cos＜\overrightarrow{ED}，\overrightarrow{CD}＞$=2•2cos120°=-2．
故答案为：-2．
点评 考查正六边形的内角为120°，以及相对的边平行，相等向量的概念，数量积的计算公式．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
12．
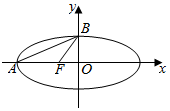如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{a}$+y2=1（a＞1）的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则a的值为（ ）
如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{a}$+y2=1（a＞1）的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则a的值为（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{1+\sqrt{5}}{2}$ | C． | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | D． | 2 |
2．己知x0=$\frac{π}{3}$是函数f（x）=sin（2x+φ）的一个极大值点，则f（x）的一个单调递减区间是（ ）
| A． | （$\frac{π}{6}$，$\frac{2π}{3}$） | B． | （$\frac{π}{3}$，$\frac{5π}{6}$） | C． | （$\frac{π}{2}$，π） | D． | （$\frac{2π}{3}$，π） |
9．已知函数f（x）=sin（x-$\frac{π}{6}$）cos（x-$\frac{π}{6}$）（x∈R），则下列结论错误的是（ ）
| A． | 函数f（x）的最小正周期为π | B． | 函数f（x）的图象关于直线x=-$\frac{π}{12}$对称 | ||
| C． | 函数f（x）的图象关于点（-$\frac{π}{6}$，0）对称 | D． | 函数f（x）在区间[0，$\frac{5π}{12}$]上是增函数 |