题目内容
17.设数列{an}的前几项的Sn=n(5-n),求通项公式an.分析 利用an=Sn-Sn-1代入计算,进而可得结论.
解答 解:依题意,当n≥2时,an=Sn-Sn-1
=n(5-n)-(n-1)(6-n)=-2n+6,
又∵当n=1时,a1=S1=4满足上式,
∴an=-2n+6.
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
7.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64人,数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(1)设在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)已知a≥8,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
X 人数 Y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(1)设在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)已知a≥8,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
12.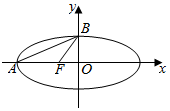 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )
 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | D. | 2 |
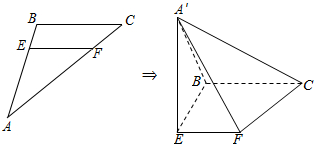 已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AE=2EB,AF=2FC,将△AEF沿EF折起,使A变到A′,使平面A′EF⊥平面EFCB.
已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AE=2EB,AF=2FC,将△AEF沿EF折起,使A变到A′,使平面A′EF⊥平面EFCB.