题目内容
7.数列{an}是递增数列,且满足an+1=f(an),a1∈(0,1),则f(x)不可能是( )| A. | f(x)=$\sqrt{x}$ | B. | f(x)=2x-1 | C. | f(x)=$\sqrt{2x-{x}^{2}}$ | D. | f(x)=log2(x+1) |
分析 A.由a1∈(0,1),可得${a}_{n+1}=\sqrt{{a}_{n}}$>an,即可判断出数列{an}的单调性;
B.由a1∈(0,1),不妨取a1=$\frac{1}{2}$,则a2=${2}^{\frac{1}{2}}$-1=$\sqrt{2}$-1$<\frac{1}{2}$,即可判断出数列{an}的单调性;
C:f(x)=$\sqrt{2x-{x}^{2}}$,令2x-x2≥0,可得得0≤x≤2.由f(x)=$\sqrt{2x-{x}^{2}}$=$\sqrt{1-(x-1)^{2}}$,利用二次函数的单调性及其a1∈(0,1),即可判断出数列{an}的单调性;
D.利用几何画板画出图象y=log2(x+1),y=x,可知:在x∈(0,1)时,log2(x+1)>x,即可判断出数列{an}的单调性.
解答 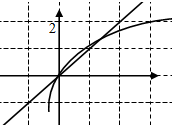 解:对于A.∵a1∈(0,1),∴${a}_{n+1}=\sqrt{{a}_{n}}$>an,可得数列{an}是递增数列
解:对于A.∵a1∈(0,1),∴${a}_{n+1}=\sqrt{{a}_{n}}$>an,可得数列{an}是递增数列
对于B.∵a1∈(0,1),不妨取a1=$\frac{1}{2}$,则a2=${2}^{\frac{1}{2}}$-1=$\sqrt{2}$-1$<\frac{1}{2}$,因此数列{an}不是递增数列;
对于C:f(x)=$\sqrt{2x-{x}^{2}}$,令2x-x2≥0,解得0≤x≤2.由f(x)=$\sqrt{2x-{x}^{2}}$=$\sqrt{1-(x-1)^{2}}$,可知:当0≤x≤1时,函数f(x)单调递增;当1≤x≤2时,函数f(x)单调递减.∵a1∈(0,1),∴数列{an}是递增数列;
对于D.利用几何画板画出图象y=log2(x+1),y=x,可知:在x∈(0,1)时,log2(x+1)>x,
∴an+1=log2(an+1)>an,因此数列{an}是递增数列.
故选:B.
点评 本题考查了数列的单调性,考查了数形结合方法、推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案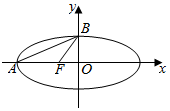 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则a的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | D. | 2 |
| A. | 函数f(x)的最小正周期为π | B. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | ||
| C. | 函数f(x)的图象关于点(-$\frac{π}{6}$,0)对称 | D. | 函数f(x)在区间[0,$\frac{5π}{12}$]上是增函数 |