题目内容
3．“a=2”是“直线2x-3y=0与直线3x+ay+1=0垂直”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 对a分类讨论，利用两条直线相互垂直的充要条件即可得出．
解答 解：a=0时，两条直线不垂直．
当a≠0时，若两条直线垂直，则-$\frac{2}{-3}$×$（-\frac{3}{a}）$=-1，解得a=2．
∴“a=2”是“直线2x-3y=0与直线3x+ay+1=0垂直”的充要条件．
故选：C．
点评 本题考查了两条直线相互垂直的充要条件、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．若集合M={x|$\frac{1}{x}$＜2}，集合N={x|-1＜x＜2}，则M∩N等于（ ）
| A． | {x|$\frac{1}{2}$＜x＜2} | B． | {x|-1＜x＜0或$\frac{1}{2}$＜x＜2} | C． | {x|-1＜x＜$\frac{1}{2}$} | D． | {x|0＜x＜$\frac{1}{2}$或1＜x＜2} |
12．
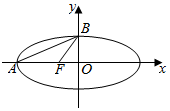如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{a}$+y2=1（a＞1）的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则a的值为（ ）
如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{a}$+y2=1（a＞1）的左顶点为A，左焦点为F，上顶点为B，若∠BAO+∠BFO=90°，则a的值为（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{1+\sqrt{5}}{2}$ | C． | $\sqrt{\frac{1+\sqrt{5}}{2}}$ | D． | 2 |