题目内容
用适当的方法表示下列集合.
(1)方程x(x2+2x+1)=0的解;
(2)不等式x-3>4的解集.
(1)方程x(x2+2x+1)=0的解;
(2)不等式x-3>4的解集.
考点:集合的表示法
专题:集合
分析:(1)根据方程根的个数为有限个,且个数不多,故解方程后用列举法表示;
(2)根据不等式的解有无限个,且有规律可循,故解不等式后用性质描述法表示.
(2)根据不等式的解有无限个,且有规律可循,故解不等式后用性质描述法表示.
解答:
解:(1)解方程x(x2+2x+1)=0得:
x=0或x=-1,
故方程x(x2+2x+1)=0的解集为{-1,0};
(2)解不等式x-3>4得:x>7,
故不等式x-3>4的解集为{x|x>7}.
x=0或x=-1,
故方程x(x2+2x+1)=0的解集为{-1,0};
(2)解不等式x-3>4得:x>7,
故不等式x-3>4的解集为{x|x>7}.
点评:本题考查的知识点是集合的表示,熟练掌握集合表示方法的适用范围是解答的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
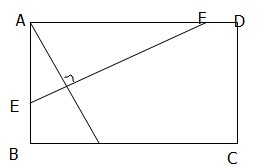 如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.
如图所示,已知正方形ABCD的边长为32cm,点P在BC上,且BP=16cm,EF⊥AP且与AB、CD分别相交于E、F两点,求EF的长.