题目内容
已知函数f(x)=x2-2alnx(a∈R且a≠0)
(1)当实数a=1时,求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,2]上的最小值.
(1)当实数a=1时,求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,2]上的最小值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)a=1时,f(x)=x2-2lnx,得f′(x)=2x-
,从而f(x)在(0,1)递减,在(1,+∞)递增;
(2)先求出f′(x)=2x-
,再分别讨论①a<0时,②a>0时的情况,从而求出函数在[1,2]上的最小值.
| 2 |
| x |
(2)先求出f′(x)=2x-
| 2a |
| x |
解答:
解:(1)a=1时,f(x)=x2-2lnx,
∴f′(x)=2x-
,
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)∵f′(x)=2x-
,
①a<0时,f′(x)>0,f(x)在[1,2]递增,
∴f(x)在[1,2]上的最小值为:f(1)=1,
②a>0时,
令f′(x)>0,解得:x>
,
令f′(x)<0,解得:0<x<
,
∴f(x)在(0,
)递减,在(
,+∞)递增,
当
≤1时,f(x)在[1,2]上的最小值为:f(1)=1,
当
>1时,f(x)在[1,2]上的最小值为:f(
)=a-alna.
∴f′(x)=2x-
| 2 |
| x |
令f′(x)>0,解得:x>1,
令f′(x)<0,解得:0<x<1,
∴f(x)在(0,1)递减,在(1,+∞)递增;
(2)∵f′(x)=2x-
| 2a |
| x |
①a<0时,f′(x)>0,f(x)在[1,2]递增,
∴f(x)在[1,2]上的最小值为:f(1)=1,
②a>0时,
令f′(x)>0,解得:x>
| a |
令f′(x)<0,解得:0<x<
| a |
∴f(x)在(0,
| a |
| a |
当
| a |
当
| a |
| a |
点评:本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
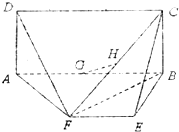 已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB∥FE,G、H分别为AB、CF的中点,AB=2,AD=EF=1,∠AFB=
已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB∥FE,G、H分别为AB、CF的中点,AB=2,AD=EF=1,∠AFB=