题目内容
16.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是(以下k∈Z)( )| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π] | B. | [kπ-$\frac{3}{8}$π,kπ+$\frac{π}{8}$] | C. | [2kπ+$\frac{π}{8}$,2kπ+$\frac{5}{8}$π] | D. | [2kπ-$\frac{3}{8}$π,2kπ+$\frac{π}{8}$] |
分析 由条件利用诱导公式,余弦函数的单调性,求得函数y的减区间.
解答 解:函数y=cos($\frac{π}{4}$-2x)=cos(2x-$\frac{π}{4}$),令2kπ≤2x-$\frac{π}{4}$≤2kπ+π,
求得kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,可得它的单调递减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z,
故选:A.
点评 本题主要考查诱导公式,余弦函数的单调性,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.已知全集U=R,A={x|x>1},B={x|x<0},则集合(∁UA)∩(∁UB)=( )
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {x|0<x<1} | D. | {x|0≤x≤1} |
7.已知sin(α+β)=$\frac{1}{2},sin(α-β)=\frac{1}{10}$,则tanαcotβ=( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
8.函数y=$\sqrt{-{x^2}+4x-3}$的定义域是( )
| A. | (-∞,1] | B. | [3,+∞) | C. | [1,3] | D. | (-∞,1]∪[3,+∞) |
5.函数g(x)=ax3+2x2+3ax在区间(-∞,$\frac{a}{3}$)内单凋递减,则a的取值范围是( )
| A. | (-∞,0] | B. | [$-\frac{2}{3}$,$\frac{2}{3}$] | C. | (-∞,-$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$) |
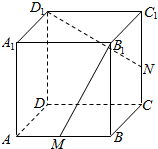 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题: