题目内容
11.计算:(Ⅰ)${log_5}25+lg\frac{1}{100}+ln\sqrt{e}+{2^{{{log}_2}3}}$(Ⅱ)${(\frac{9}{4})^{0.5}}+{(-3)^{-1}}÷{0.75^{-2}}$.
分析 根据指数幂的运算法则和对数的运算法则计算即可.
解答 解:(Ⅰ)原式=$2+(-2)+\frac{1}{2}+3=\frac{7}{2}$,
(Ⅱ)原式=$\frac{3}{2}-\frac{1}{3}×\frac{9}{16}=\frac{21}{16}$.
点评 本题考查了指数幂的运算法则和对数的运算法则,属于基础题.

练习册系列答案
相关题目
1.已知直线l在x轴上的截距为3,在y轴上的截距为-2,则l的方程为( )
| A. | 3x-2y-6=0 | B. | 2x-3y+6=0 | C. | 2x-3y-6=0 | D. | 3x-2y+6=0 |
2.△ABC的三边a,b,c成等差数列,则角B的范围是( )
| A. | $({0,\frac{π}{3}}]$ | B. | $[{\frac{π}{6},\frac{π}{2}})$ | C. | $[{\frac{π}{4},\frac{π}{2}})$ | D. | $({0,\frac{π}{2}})$ |
6.函数$f(x)=\frac{{-{{tan}^2}x-tanx}}{1+tanx}$的奇偶性为( )
| A. | 既奇又偶函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 奇函数 |
16.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是(以下k∈Z)( )
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π] | B. | [kπ-$\frac{3}{8}$π,kπ+$\frac{π}{8}$] | C. | [2kπ+$\frac{π}{8}$,2kπ+$\frac{5}{8}$π] | D. | [2kπ-$\frac{3}{8}$π,2kπ+$\frac{π}{8}$] |
3.曲线y=x3-2x在点(1,-1)处的切线倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
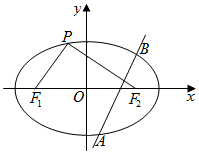 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=$\frac{{\sqrt{2}}}{2}$,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为2.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率e=$\frac{{\sqrt{2}}}{2}$,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为2.