题目内容
14.若直线l与曲线M(x0,y0)满足下列两个条件:(1)直线l在点M(x0,y0)处与曲线C相切;
(2)曲线C在点M附近位于直线l的两侧,则称直线l在点M处“内切”曲线C.
下列命题正确的是①②(写出所有正确命题的编号)
①直线l:y=0在点M(0,0)处“内切”曲线C:y=x3
②直线l:y=x在点M(0,0)处“内切”曲线C:y=sinx
③直线l:y=x-1在点M(1,0)处“内切”曲线C:y=lnx.
分析 分别求出每一个命题中曲线C的导数,得到曲线在点M处的导数值,求出曲线在点M处的切线方程,再由曲线在点M两侧的函数值与对应直线上点的值的大小判断是否满足条件(2),则正确的选项可求.
解答 解:①,由y=x3,得y′=3x2,则y′|x=0=0,直线y=0是在点M(0,0)处的曲线C的切线,
又当x>0时y>0,当x<0时y<0,满足曲线C在M(0,0)附近位于直线y=0两侧,故命题①正确;
②,由y=sinx,得y′=cosx,则y′|x=0=1,直线y=x是在点M(0,0)处的曲线的切线,
满足曲线C在M(0,0)附近位于直线y=x两侧,故命题②正确;
③,由y=lnx,得y′=$\frac{1}{x}$,则y′|x=1=1,曲线在M(1,0)处的切线为y=x-1,
由g(x)=x-1-lnx,得g′(x)=1-$\frac{1}{x}$,当x∈(0,1)时,g′(x)<0,当x∈(1,+∞)时,
g′(x)>0.则g(x)在(0,+∞)上有极小值也是最小值,为g(1)=0.
即y=x-1恒在y=lnx的上方,不满足曲线C在点M附近位于直线l的两侧,故命题③错误.
故答案为:①②.
点评 本题考查命题的真假判断与应用,考查了利用导数研究过曲线上某点处的切线方程,综合考查导数的应用.

练习册系列答案
相关题目
19.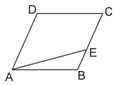 已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
 已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )| A. | $\frac{1}{3}$ | B. | $\frac{9}{16}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
3.某个命题与自然数有关,如果当n=k(k∈N*)时该命题成立,那么可以推得n=k+1时该命题也成立.现已知n=5时该命题不成立,那么( )
| A. | n=4时该命题不成立 | |
| B. | n=6时该命题不成立 | |
| C. | n为大于5的某个自然数时该命题成立 | |
| D. | 以上答案均不对 |
4.(1+i)(2+i)=( )
| A. | 1-i | B. | 1+3i | C. | 3+i | D. | 3+3i |
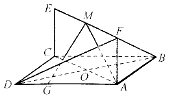 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G为线段AD上的任意一点.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G为线段AD上的任意一点.