题目内容
9.已知数列a1,a2-a1,a3-a2,…,an-an-1,…是首项为1,公差为1的等差数列,则数列{an}的通项公式an=$\frac{1}{2}$n(n+1).分析 利用累加法可知当n≥2时an=n+$\frac{n(n-1)}{2}$,进而验证当n=1是否成立即可.
解答 解:因为a1,a2-a1,a3-a2,…,an-an-1,…是首项为1、公差为1的等差数列,
所以当n≥2时an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=n+$\frac{n(n-1)}{2}$,
又因为a1=1满足上式,
所以${a_n}=\frac{1}{2}n(n+1)$,
故答案为:$\frac{1}{2}$n(n+1).
点评 本题考查数列的通项及前n项和,考查累加法,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.已知a,b∈R,则“|a|+|b|>1”是“b<-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
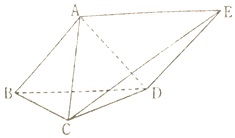 如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.
如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直. 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.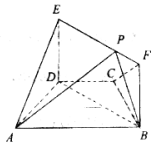 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.