题目内容
6.已知函数f(x)=|$\overrightarrow{MP}$-x$\overrightarrow{MN}$|(x∈R),其中MN是半径为4的圆O的一条弦,O为原点,P为单位圆上的点,设函数f(x)的最小值为t,当点P在单位圆上运动时,t的最大值为3,则线段MN的长度为4$\sqrt{3}$.分析 设x$\overrightarrow{MN}$=$\overrightarrow{MA}$,函数f(x)的最小值化为点P到直线MN的距离,结合图形求出tmax=3时MN的长度.
解答 解:设x$\overrightarrow{MN}$=$\overrightarrow{MA}$,
则函数f(x)=|$\overrightarrow{MP}$-x$\overrightarrow{MN}$|=|$\overrightarrow{MP}$-$\overrightarrow{MA}$|=|$\overrightarrow{AP}$|,其中P为单位圆O上的点,
∵x$\overrightarrow{MN}$=$\overrightarrow{MA}$,
∴点A在直线MN上;
∴函数f(x)的最小值t为点P到直线MN的距离,
当tmax=3时,如图所示;
线段MN的长度为|MN|=2$\sqrt{{4}^{2}-(3-1)^{2}}$=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了向量知识的运用问题,也考查了转化思想与数形结合的应用问题,是综合题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.已知m,n,l是三条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m?α,n?α,n⊥l,则l⊥α | ||
| C. | 若m∥α,n⊥β,α⊥β,则m∥n | D. | 若l⊥α,l⊥β,则α∥β |
1.已知a,b∈R,则“|a|+|b|>1”是“b<-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
15.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
| A. | f(x)=2-x | B. | f(x)=x2 | C. | f(x)=3-x | D. | f(x)=cosx |
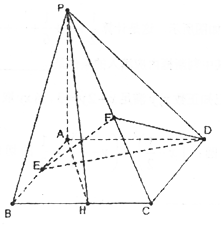 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点.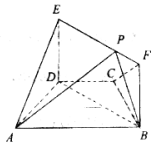 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.