题目内容
5.已知定义在R上的奇函数f(x),当x>0时,f(x)=log2(x+1),则使得f(2x)<f(x-1)成立的x的取值范围为{x|x<-1}.分析 求出函数的解析式,结合函数奇偶性,判断函数的单调性,利用函数单调性的性质将不等式进行转化是解决本题的关键.
解答 解:定义在R上的奇函数f(x),则f(0)=0,
当x>0时,f(x)=log2(x+1)为增函数,且此时f(x)>0,
当x<0,则-x>0,此时f(-x)=log2(-x+1)=-f(x),
即当x<0时,f(x)=-log2(-x+1),此时函数为增函数,且f(x)<0,
综上f(x)在R为增函数,
则不等式f(2x)<f(x-1)等价为2x<x-1,即x<-1,
故答案为:{x|x<-1}.
点评 本题主要考查不等式的求解,结合函数奇偶性的性质,判断函数的单调性是解决本题的关键.

练习册系列答案
相关题目
15.某体育彩票规定:从01到36个号中抽出7个号为一注,每注2元.某人想先选定吉利号18,然后再从01到17个号中选出3个连续的号,从19到29个号中选出2个连续的号,从30到36个号中选出1个号组成一注.若这个人要把这种要求的号全买,至少要花的钱数为( )
| A. | 2000元 | B. | 3200元 | C. | 1800元 | D. | 2100元 |
16.已知m,n,l是三条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m?α,n?α,n⊥l,则l⊥α | ||
| C. | 若m∥α,n⊥β,α⊥β,则m∥n | D. | 若l⊥α,l⊥β,则α∥β |
15.若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质,下列函数中具有M性质的是( )
| A. | f(x)=2-x | B. | f(x)=x2 | C. | f(x)=3-x | D. | f(x)=cosx |
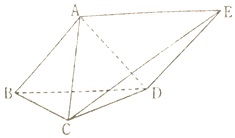 如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.
如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.