题目内容
△ABC的三个内角A,B,C所对的边长分别为a,b,c,设向量
=(sinB,a+c),
=(sinC-sinA,b-a).若?λ∈R,使
=λ
,则∠C的大小为 .
| p |
| q |
| p |
| q |
考点:正弦定理,平行向量与共线向量,余弦定理
专题:解三角形
分析:利用向量共线定理、正弦定理、余弦定理即可得出.
解答:
解:∵?λ∈R,使
=λ
,
∴(a+c)(sinC-sinA)=(b-a)sinB,
∴(a+c)(c-a)=(b-a)b,
∴a2+b2-c2=ab.
∴cosC=
=
.
∵C∈(0,π),
∴C=
.
故答案为:
.
| p |
| q |
∴(a+c)(sinC-sinA)=(b-a)sinB,
∴(a+c)(c-a)=(b-a)b,
∴a2+b2-c2=ab.
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵C∈(0,π),
∴C=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查了余弦定理、正弦定理、向量共线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
若P是长度为6的线段AB上任意一点,则点P到线段AB两端距离均不小于1的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知i为虚数单位,则复数
等于( )
| 2 |
| 1-i |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
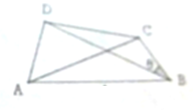 如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.
如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.