Question

已知抛物线y²=2px（p＞0）的焦点为F，点P为抛物线上的动点，点M为其准线上的动点，若△FPM为边长是12的等边三角形，则此抛物线方程为

 

．

Answer 1

考点：抛物线的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：利用抛物线的定义得出PM垂直于抛物线的准线，设（

m2

2p

，m），求出△PMF的边长，写出有关点的坐标，利用两点距离的公式得到FM，列出方程求出m、p的值，得到抛物线方程．

解答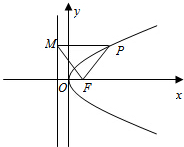： 解：据题意知，△PMF为等边三角形，PF=PM，
∴PM⊥抛物线的准线，
设P（

m2

2p

，m），则M（-

p

2

，m），
等边三角形边长为

m2

2p

+

p

2

=12，F（

p

2

，0）
所以由PM=FM，得

p2+m2

=12，解得p=6，m=6

3

，
∴抛物线方程为y²=12x．
故答案为：y²=12x．

点评：本题主要考查了抛物线的简单性质，直线与抛物线的综合问题．考查了学生综合把握所学知识和基本的运算能力．