题目内容
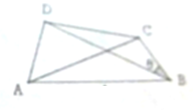 如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.
如图所示,在平面四边形ABCD中,AB=4,AD=2,∠DAB=60°,∠BCD=120°.(1)当BC=CD时,求△BCD的面积;
(2)设∠CDB=θ,记四边形ABCD的周长为f(θ),求f(θ)的方程,并求出它的最大值.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)在△ABD中,由余弦定理可得BD,在△BCD中由正弦定理可得BC,由面积公式可得;
(2)在△BCD中,由正弦定理可得
=
=
=4,可得DC=4sinθ,BC=4sin(60°-θ),可得f(θ)=4sin(θ+60°)+6,由三角函数的最值可得.
(2)在△BCD中,由正弦定理可得
| DC |
| sinθ |
| BC |
| sin(60°-θ) |
| BD |
| sin120° |
解答:
解:(1)在△ABD中,AB=4,AD=2,∠DAB=60°,
由余弦定理可得BD=
=2
,
在△BCD中,∠BCD=120°,∴当BC=CD时,∠BDC=30°,
∴由正弦定理可得BC=
=
=2,
∴△BCD的面积S=
×BC×CD×sin∠BCD=
×2×2×
=
;
(2)在△BCD中,由正弦定理可得
=
=
=4,
解得DC=4sinθ,BC=4sin(60°-θ),
∴f(θ)=AB+AD+BC+CD=6+4sinθ+4sin(60°-θ)
=4sinθ+2
cosθ-2sinθ+6=4sin(θ+60°)+6,
∵0°<θ<60°,∴当且即当θ=30°时,sin(θ+60°)有最大值1,
∴f(θ)的最大值为:10.
由余弦定理可得BD=
22+42-2×2×4×
|
| 3 |
在△BCD中,∠BCD=120°,∴当BC=CD时,∠BDC=30°,
∴由正弦定理可得BC=
| BDsin30° |
| sin120° |
2
| ||||
|
∴△BCD的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
(2)在△BCD中,由正弦定理可得
| DC |
| sinθ |
| BC |
| sin(60°-θ) |
| BD |
| sin120° |
解得DC=4sinθ,BC=4sin(60°-θ),
∴f(θ)=AB+AD+BC+CD=6+4sinθ+4sin(60°-θ)
=4sinθ+2
| 3 |
∵0°<θ<60°,∴当且即当θ=30°时,sin(θ+60°)有最大值1,
∴f(θ)的最大值为:10.
点评:本题考查解三角形的实际应用,涉及正余弦定理的应用,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知i为虚数单位,若数列{an}满足:a1=i,且(1-i)an+1=(1+i)an,则复数a5=( )
| A、-i | B、-1 | C、i | D、1 |
设随机变量ξ服从正态分布 N(μ,σ2),若方程x2+4x+ξ=0没有实根的概率是
,则μ=( )
| 1 |
| 2 |
| A、1 | B、2 | C、4 | D、不能确定 |
已知x,y满足
,则x-y+1的取值范围是( )
|
| A、[-2,2] |
| B、[-1,2] |
| C、[-2,e] |
| D、[-1,e] |