题目内容
1.已知4x2+y2=4,则$\frac{y}{x+2}$最大值为$\frac{2\sqrt{3}}{3}$.分析 $\frac{y}{x+2}$的几何意义是点(x,y)与点(-2,0)连线的斜率,结合图象解得.
解答 解:∵4x2+y2=4,∴x2+$\frac{{y}^{2}}{4}$=1,
作图象如下,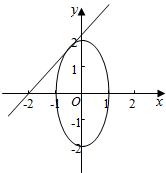 ,
,
设$\frac{y}{x+2}$=k,则y=k(x+2),
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{4{x}^{2}+{y}^{2}=4}\end{array}\right.$化简可得,
(4+k2)x2+4k2x+4k2-4=0,
令△=(4k2)2-4(4+k2)(4k2-4)=0,
解得,k=±$\frac{2\sqrt{3}}{3}$,
故$\frac{y}{x+2}$最大值为$\frac{2\sqrt{3}}{3}$;
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了数形结合的思想应用及斜率的应用,同时考查了学生的作图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设a>0,且a≠1,则“a>1”是“loga$\frac{1}{2}$<1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知$a={log_{\frac{1}{3}}}5$,b=0.53,$c={log_{\frac{1}{5}}}3$,则a,b,c三者的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | a<c<b | D. | a<b<c |
16.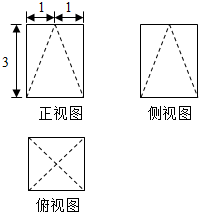 一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )
一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )
 一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )
一个几何体的三视图如图所示,正视图与侧视图为全等的矩形,俯视图为正方形,则该几何体的体积为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |