题目内容
11．设a＞0，且a≠1，则“a＞1”是“loga$\frac{1}{2}$＜1”的（ ）| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 把1变成底数的对数，讨论底数与1的关系，确定函数的单调性，根据函数的单调性整理出关于a的不等式，得到结果，把两种情况求并集得到结果．
解答 解：∵loga$\frac{1}{2}$＜1=logaa，
当a＞1时，函数是一个增函数，不等式成立，
当0＜a＜1时，函数是一个减函数，根据函数的单调性有a＜$\frac{1}{2}$，
综上可知a的取值是（0，$\frac{1}{2}$）∪（1，+∞），
故“a＞1”是“loga$\frac{1}{2}$＜1”的充分不必要条件，
故选：A．
点评 本题主要考查对数函数单调性的应用、不等式的解法等基础知识，本题解题的关键是对于底数与1的关系，这里应用分类讨论思想来解题．
练习册系列答案
相关题目
2．已知几何体的三视图（如图），则该几何体的表面积为（ ）
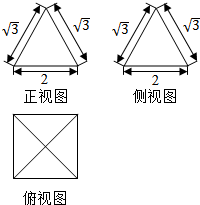
| A． | $4\sqrt{2}$ | B． | $4\sqrt{3}$ | C． | 4$\sqrt{2}$+4 | D． | 4$\sqrt{3}$+4 |
19．
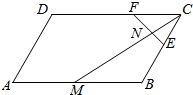如图平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{d}$，F是CD的三等分点，E是BC中点，M是AB中点，MC∩EF=N，若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$，则λ1+λ2=（ ）
如图平行四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{b}$，$\overrightarrow{AD}$=$\overrightarrow{d}$，F是CD的三等分点，E是BC中点，M是AB中点，MC∩EF=N，若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$，则λ1+λ2=（ ）| A． | $\frac{15}{14}$ | B． | 1 | C． | $\frac{5}{14}$ | D． | -$\frac{5}{14}$ |
6．在平面直角坐标系中，过点（0，1）且倾斜角为45°的直线不经过（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．
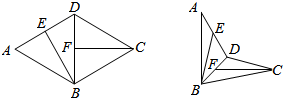如图，在菱形ABCD中，∠BAD=60°，线段AD，BD的中点分别为E，F．现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是（ ）
如图，在菱形ABCD中，∠BAD=60°，线段AD，BD的中点分别为E，F．现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是（ ）| A． | （$\frac{π}{6}$，$\frac{π}{3}$） | B． | （$\frac{π}{6}$，$\frac{π}{2}$] | C． | （$\frac{π}{3}$，$\frac{π}{2}$] | D． | （$\frac{π}{3}$，$\frac{2π}{3}$） |
3．已知焦点在y轴上的双曲线$\frac{{x}^{2}}{m}$+y2=1，其准线方程为y=±$\frac{\sqrt{5}}{5}$，则实数m的值是（ ）
| A． | -4 | B． | -$\frac{1}{4}$ | C． | -4或-$\frac{1}{4}$ | D． | -$\frac{1}{2}$ |
20．函数y=2sin（3x+$\frac{π}{6}$），x∈R的最小正周期是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{3π}{2}$ | D． | π |