题目内容
6.(1)已知正数x、y满足xy=x+y+3,试求xy、x+y的范围.(2)已知x>0,求证:x+$\frac{1}{x}$+$\frac{1}{x+\frac{1}{x}}$≥$\frac{5}{2}$.
分析 (1)由xy=x+y+3≥2$\sqrt{xy}$+3,解不等式即可得到xy,x+y的范围;
(2)设t=x+$\frac{1}{x}$≥2,运用t+$\frac{1}{t}$的导数1-$\frac{1}{{t}^{2}}$>0,可得单调性,进而得证.
解答 解:(1)由正数x、y满足xy=x+y+3,
可得xy=x+y+3≥2$\sqrt{xy}$+3,
设t=$\sqrt{xy}$(t>0),可得t2-2t-3≥0,
解得t≥3,即有xy≥9,
可得x+y≥6,当且仅当x=y=3,取得等号.
则xy的范围是[9,+∞),x+y的范围是[6,+∞);
(2)证明:设t=x+$\frac{1}{x}$≥2(当且仅当x=1时,等号成立),
即有t+$\frac{1}{t}$的导数1-$\frac{1}{{t}^{2}}$>0在[2,+∞)恒成立,
即有t+$\frac{1}{t}$≥2+$\frac{1}{2}$=$\frac{5}{2}$(当且仅当t=2即x=1取得等号),
则x+$\frac{1}{x}$+$\frac{1}{x+\frac{1}{x}}$≥$\frac{5}{2}$.
点评 本题考查基本不等式的运用:求取值范围和证明不等式,注意满足的条件:一正二定三等,考查运算能力,属于中档题.

练习册系列答案
相关题目
16.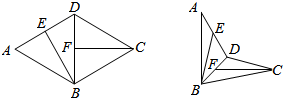 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
 如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )
如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是( )| A. | ($\frac{π}{6}$,$\frac{π}{3}$) | B. | ($\frac{π}{6}$,$\frac{π}{2}$] | C. | ($\frac{π}{3}$,$\frac{π}{2}$] | D. | ($\frac{π}{3}$,$\frac{2π}{3}$) |
18.函数f(x)=x(x+1)的图象在点x=1处的切线方程为( )
| A. | 3x-y-1=0 | B. | 3x-y-5=0 | C. | 3x-y+5=0 | D. | 3x+y-1=0 |