题目内容
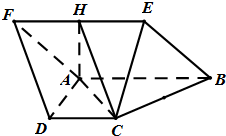 如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.(1)求证:平面AHC⊥平面BCE;
(2)求此几何体的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)由已知条件推导出AH⊥AB,AH⊥BC,AC⊥BC,从而得到BC⊥面AHC,由此能证明面AHC⊥面BCE.
(2)V=VE-ACB+VF-ADC+VC-AEF.
(2)V=VE-ACB+VF-ADC+VC-AEF.
解答:
(1)证明:在菱形ABEF中,因为∠ABE=60°,所以△AEF是等边三角形,
又因为H是线段EF的中点,所以AH⊥EF⇒AH⊥AB
因为面ABEF⊥面ABCD,且面ABEF∩面ABCD=AB,
所以AH⊥面ABCD,所以AH⊥BC,
在直角梯形中,AB=2AD=2CD=4,∠BAD=∠CDA=90°,得到AC=BC=2
,
从而AC2+BC2=AB2,所以AC⊥BC,又AH∩AC=A
所以BC⊥面AHC,
又BC?面BCE,所以平面AHC⊥平面BCE….(6分)
(2)解:因为V=VE-ACB+VF-ADC+VC-AEF,
S△ACB=4,S△ADC=2,S△AEF=4
所以V=VE-ACB+VF-ADC+VF-ACE=
(2
×4+2
×2+2×4
)=
..(12分)
又因为H是线段EF的中点,所以AH⊥EF⇒AH⊥AB
因为面ABEF⊥面ABCD,且面ABEF∩面ABCD=AB,
所以AH⊥面ABCD,所以AH⊥BC,
在直角梯形中,AB=2AD=2CD=4,∠BAD=∠CDA=90°,得到AC=BC=2
| 2 |
从而AC2+BC2=AB2,所以AC⊥BC,又AH∩AC=A
所以BC⊥面AHC,
又BC?面BCE,所以平面AHC⊥平面BCE….(6分)
(2)解:因为V=VE-ACB+VF-ADC+VC-AEF,
S△ACB=4,S△ADC=2,S△AEF=4
| 3 |
所以V=VE-ACB+VF-ADC+VF-ACE=
| 1 |
| 3 |
| 3 |
| 3 |
| 3 |
20
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查几何体的体积的计算,正确运用平面与平面垂直的判定定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若实数a,b,c,d满足a>b,c>d,则下列不等式成立的是( )
| A、a-c>b-d | ||||
| B、a+c>b+d | ||||
| C、ac>bd | ||||
D、
|
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N. 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=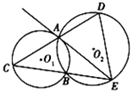 已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.
已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.