题目内容
已知数列{an}的前n项和Sn=n2-13n+1.
(1)求数列的通项公式;
(2)求Sn的最大或最小值.
(1)求数列的通项公式;
(2)求Sn的最大或最小值.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”即可得出数列的通项公式.
(2)利用二次函数与数列的前n项和的关系,求出数列Sn的最小值.
(2)利用二次函数与数列的前n项和的关系,求出数列Sn的最小值.
解答:
解:(1)当n=1时,a1=S1=1-13+1=-11.
当n≥2时,an=Sn-Sn-1=n2-13n+1-[(n-1)2-13(n-1)+1]=2n-14.
∴an=
.
(2)∵Sn=n2-13n+1=(n-
)2-
,其图象是以n=
为对称轴,开口向上的抛物线上的孤立点,
∵n∈N+,
∴Sn的最小值为S6=S7=-41.没有最大值.
当n≥2时,an=Sn-Sn-1=n2-13n+1-[(n-1)2-13(n-1)+1]=2n-14.
∴an=
|
(2)∵Sn=n2-13n+1=(n-
| 13 |
| 2 |
| 165 |
| 4 |
| 13 |
| 2 |
∵n∈N+,
∴Sn的最小值为S6=S7=-41.没有最大值.
点评:(1)主要考查了利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”是解题的关键,(2)主要考查了求解数列和的最小值问题,主要利用二次函数的基本性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
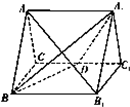 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.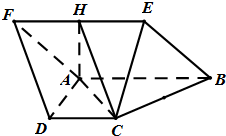 如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.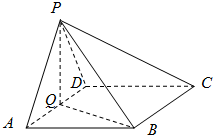 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.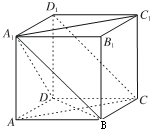 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.