题目内容
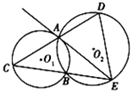 已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.
已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.(Ⅰ)如图,当点D与点A不重合时,证明:EA=ED;
(Ⅱ)当点D与点A重合时,若BC=2,CE=8,求⊙O1的直径.
考点:与圆有关的比例线段
专题:立体几何
分析:(Ⅰ)连结AB,在EA延长线上取一点F,由弦切角定理得∠FAC=∠ABC,又∠ABC是⊙O2内接四边形ABED外角,由此能证明EA=ED.
(Ⅱ)当D与A重合时,CA与⊙O2只有一个公共点,由已知条件推导出AC、AE分别是⊙O1,⊙O2的直径,由此能求出⊙O1的直径.
(Ⅱ)当D与A重合时,CA与⊙O2只有一个公共点,由已知条件推导出AC、AE分别是⊙O1,⊙O2的直径,由此能求出⊙O1的直径.
解答:
 (Ⅰ)证明:连结AB,在EA延长线上取一点F,
(Ⅰ)证明:连结AB,在EA延长线上取一点F,
∵AE是⊙O1的切线,∴∠FAC=∠ABC,
又∠ABC是⊙O2内接四边形ABED外角,
∴∠ABC=∠ADE,∴DAE=∠ADE,
∴EA=ED.
(Ⅱ)当D与A重合时,CA与⊙O2只有一个公共点,
∴CA与⊙O2相切,∠FAC=∠ARC,∠DAE=∠ARE,
∵∠FAC=∠DAE,∴AC、AE分别是⊙O1,⊙O2的直径,
由AC2=CB•CE=2×8=16,
∴AC=4,即⊙O1的直径为4.
 (Ⅰ)证明:连结AB,在EA延长线上取一点F,
(Ⅰ)证明:连结AB,在EA延长线上取一点F,∵AE是⊙O1的切线,∴∠FAC=∠ABC,
又∠ABC是⊙O2内接四边形ABED外角,
∴∠ABC=∠ADE,∴DAE=∠ADE,
∴EA=ED.
(Ⅱ)当D与A重合时,CA与⊙O2只有一个公共点,
∴CA与⊙O2相切,∠FAC=∠ARC,∠DAE=∠ARE,
∵∠FAC=∠DAE,∴AC、AE分别是⊙O1,⊙O2的直径,
由AC2=CB•CE=2×8=16,
∴AC=4,即⊙O1的直径为4.
点评:本题考查线段长的求法,考查圆的直径的求法,解题时要认真审题,注意弦切角定理的合理运用.

练习册系列答案
相关题目
设等比数列{an}满足a1+a2=1,a3+a4=3,则a5+a6=( )
| A、6 | B、9或-9 |
| C、6或-6 | D、9 |
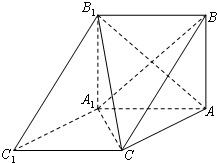 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2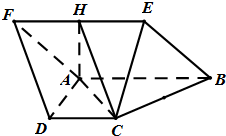 如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点. 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.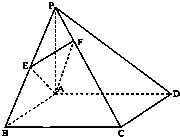 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,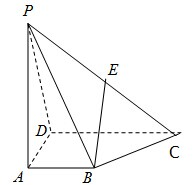 如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.
如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.