题目内容
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.(1)求证:平面SAC⊥平面AMN;
(2)求三棱锥S-ACM的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)利用面面垂直的判定定理证明平面SAC⊥平面AMN.
(2)利用VS-ACM=VD-ACM=VM-DAC,即可求三棱锥S-ACM的体积.
(2)利用VS-ACM=VD-ACM=VM-DAC,即可求三棱锥S-ACM的体积.
解答:
(1)证明:∵SA⊥底面ABCD,底面ABCD是正方形,
∴DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,
∴DC⊥AM,
又∵SA=AD,M是SD的中点,
∴AM⊥SD,
∴AM⊥平面SDC
∴SC⊥AM.
由已知AN⊥SC,
∴SC⊥平面AMN.
又SC?平面SAC,
∴平面SAC⊥平面AMN.…(6分)
(2)解:∵M是SD的中点,∴VS-ACM=VD-ACM=VM-DAC…(9分)
∴VS-ACM=
S△ACD•
SA=
•
•
=
…(12分)
∴DC⊥SA,DC⊥DA,
∴DC⊥平面SAD,
∴DC⊥AM,
又∵SA=AD,M是SD的中点,
∴AM⊥SD,
∴AM⊥平面SDC
∴SC⊥AM.
由已知AN⊥SC,
∴SC⊥平面AMN.
又SC?平面SAC,
∴平面SAC⊥平面AMN.…(6分)
(2)解:∵M是SD的中点,∴VS-ACM=VD-ACM=VM-DAC…(9分)
∴VS-ACM=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
点评:本小题主要考查空间线面关系、三棱锥S-ACM的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
记X(x y 1),T=
,X′=
,则方程XTX′=0表示的曲线只可能是( )
|
|
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
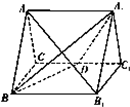 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=
如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC= 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若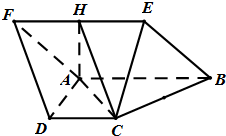 如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.