题目内容
已知点P是椭圆上一点，F1，F2为两焦点，且F1P⊥F2P，若点P到两焦点的距离分别为6和8，求椭圆的方程．
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由题意知2a=6+8=14，（2c）2=62+82=100，由此能求出椭圆方程．
解答：
（本题12分）
解：由题意知2a=6+8=14，解得a=7，…．（2分）
又F1P⊥F2P，
∴（2c）2=62+82=100，解得c2=25…．（4分）
∴b2=49-25=24，…..（6分）
当椭圆焦点在x轴上，所求方程为
+
=1，…（9分）
当椭圆焦点在y轴上，所求方程为
+
=1．…．（12分）
解：由题意知2a=6+8=14，解得a=7，…．（2分）
又F1P⊥F2P，
∴（2c）2=62+82=100，解得c2=25…．（4分）
∴b2=49-25=24，…..（6分）
当椭圆焦点在x轴上，所求方程为
| x2 |
| 49 |
| y2 |
| 24 |
当椭圆焦点在y轴上，所求方程为
| x2 |
| 24 |
| y2 |
| 49 |
点评：本题考查椭圆方程的求法，是中档题，解题时要认真审题，注意焦点坐标不同，椭圆方程不同．
练习册系列答案
阅读快车系列答案
相关题目
如图，底面是等腰梯形的四棱锥E-ABCD中，EA⊥平面ABCD，AB∥CD，AB=2CD，∠ABC=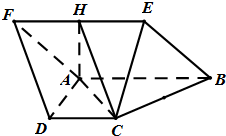
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直，AB=2AD=2CD=4，∠ABE=60°，∠BAD=∠CDA=90°，点H是线段EF的中点．
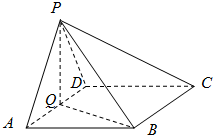如图，在四棱锥中P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
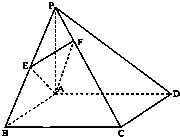如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AB，
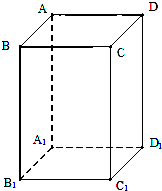已知ABCD-A1B1C1D1是底面为正方形的直四棱柱，且A1B1=1，AA1=2，求：