题目内容
若实数a,b,c,d满足a>b,c>d,则下列不等式成立的是( )
| A、a-c>b-d | ||||
| B、a+c>b+d | ||||
| C、ac>bd | ||||
D、
|
考点:不等式的基本性质
专题:不等式的解法及应用,不等式
分析:根据不等式的性质,分别将个选项分析求解即可求得答案;注意排除法在解选择题中的应用.
解答:
解:A、∵a>b,c>d,∴-c<-d,∴a+c与b+c无法比较大小,故本选项错误;
B、∵a>b,c>d,∴a+c>b-d,故本选项正确;
C、当a>b,c>d>0时,ac>bd,故本选项错误;
D、当a>b,c>d>0时,
>
,故本选项错误.
故选B.
B、∵a>b,c>d,∴a+c>b-d,故本选项正确;
C、当a>b,c>d>0时,ac>bd,故本选项错误;
D、当a>b,c>d>0时,
| a |
| d |
| b |
| c |
故选B.
点评:本题考查了不等式的性质.此题比较简单,注意解此题的关键是掌握不等式的性质:

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
一几何体的三视图如图,它的体积为( )


| A、2 | ||
B、
| ||
C、
| ||
D、
|
记X(x y 1),T=
,X′=
,则方程XTX′=0表示的曲线只可能是( )
|
|
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
若函数f(x)=logax的图象与直线y=
x相切,则a的值为( )
| 1 |
| 3 |
A、e
| ||
B、e
| ||
C、
| ||
D、e
|
已知集合A={x|x2-x-6<0},B={x|x2+2x-8>0},则A∩B=( )
| A、{x|-3<x<-2} |
| B、{x|2<x<3} |
| C、{x|-4<x<-2或2<x<3} |
| D、{x|3<x<4} |
设等比数列{an}满足a1+a2=1,a3+a4=3,则a5+a6=( )
| A、6 | B、9或-9 |
| C、6或-6 | D、9 |
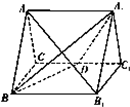 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=
如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=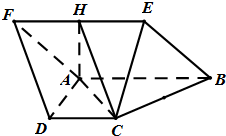 如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.