题目内容
已知点P(1+cosα,sinα),参数α∈[0,π],点Q在曲线C:ρ=
上.
(Ⅰ)求在直角坐标系中点P的轨迹方程和曲线C的方程;
(Ⅱ)求|PQ|的最小值.
| 10 | ||||
|
(Ⅰ)求在直角坐标系中点P的轨迹方程和曲线C的方程;
(Ⅱ)求|PQ|的最小值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(Ⅰ)设点P的坐标为(x,y),则有
,消去参数,结合α∈[0,π],可得点P的轨迹.根据曲线C的极坐标方程即 ρsinθ-ρcosθ=10,可得曲线C的直角坐标方程.
(Ⅱ)由题意可得点Q在直线x-y+10=0 上,点P在半圆上,求出半圆的圆心C(1,0)到直线x-y+10=0的距离,再减去1,即得所求.
|
(Ⅱ)由题意可得点Q在直线x-y+10=0 上,点P在半圆上,求出半圆的圆心C(1,0)到直线x-y+10=0的距离,再减去1,即得所求.
解答:
解:(Ⅰ)设点P的坐标为(x,y),则有
,消去参数α,
可得 (x-1)2+y2=1.
由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆:(x-1)2+y2=1 (y≥0).
∵曲线C:ρ=
,即 1=
ρ(
sinθ-
cosθ),
即 ρsinθ-ρcosθ=10,故曲线C的直角坐标方程:x-y+10=0.
(Ⅱ)由题意可得点Q在直线x-y+10=0 上,点P在半圆上,
半圆的圆心C(1,0)到直线x-y+10=0的距离等于
=
.
所以|PQ|的最小值为
-1.
|
可得 (x-1)2+y2=1.
由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆:(x-1)2+y2=1 (y≥0).
∵曲线C:ρ=
| 10 | ||||
|
| 2 |
| ||
| 2 |
| ||
| 2 |
即 ρsinθ-ρcosθ=10,故曲线C的直角坐标方程:x-y+10=0.
(Ⅱ)由题意可得点Q在直线x-y+10=0 上,点P在半圆上,
半圆的圆心C(1,0)到直线x-y+10=0的距离等于
| |1-0+10| | ||
|
11
| ||
| 2 |
所以|PQ|的最小值为
11
| ||
| 2 |
点评:本题主要考查把参数方程、极坐标化为直角坐标方程的方法,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知集合A={x|x2-x-6<0},B={x|x2+2x-8>0},则A∩B=( )
| A、{x|-3<x<-2} |
| B、{x|2<x<3} |
| C、{x|-4<x<-2或2<x<3} |
| D、{x|3<x<4} |
 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若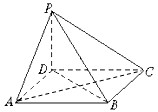 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.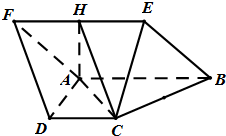 如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.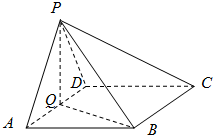 如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥中P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.