题目内容
已知圆心在y轴上的圆C经过点A(0,3)和B(4,1),过点M(-3,-3)的直线被截得弦长为4
,求直线l的方程.
| 5 |
考点:直线与圆相交的性质
专题:直线与圆
分析:求出圆的圆心与半径,设出直线方程,通过圆心到直线的距离、弦心距、半弦长满足勾股定理,即可求出直线方程.
解答:
解:圆心在y轴上的圆C经过点A(0,3)和B(4,1),
则AB的中垂线与y轴的交点就是圆C的圆心,AC的距离就是圆C的半径,
AB的中点(2,2),kAB=
=-
,
AB的中垂线的斜率为:2,中垂线方程为:y-2=2(x-2),
即2x-y-2=0.
x=0时,y=-2,圆C(0,-2),圆C的半径为:AC=5.
设过点M(-3,-3)的直线:y+3=k(x+3),即kx-y+3k-3=0.
过点M(-3,-3)的直线被截得弦长为4
,
∴圆心到直线的距离为:
=
=
,解得k=2或k=-
.
直线l的方程:2x-y+3=0或x+2y+9=0.
则AB的中垂线与y轴的交点就是圆C的圆心,AC的距离就是圆C的半径,
AB的中点(2,2),kAB=
| 1-3 |
| 4-0 |
| 1 |
| 2 |
AB的中垂线的斜率为:2,中垂线方程为:y-2=2(x-2),
即2x-y-2=0.
x=0时,y=-2,圆C(0,-2),圆C的半径为:AC=5.
设过点M(-3,-3)的直线:y+3=k(x+3),即kx-y+3k-3=0.
过点M(-3,-3)的直线被截得弦长为4
| 5 |
∴圆心到直线的距离为:
| |3k-1| | ||
|
52-(2
|
| 5 |
| 1 |
| 2 |
直线l的方程:2x-y+3=0或x+2y+9=0.
点评:本题考查直线与圆的方程的应用,圆的圆心与半径的求法,考查转化思想以及计算能力.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
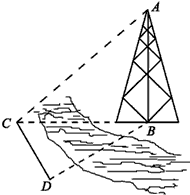 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.