题目内容
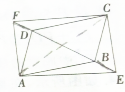
在?ABCD的对角线BD的延长线上取点E,F,使BE=DF,求证:四边形AECF是平行四边形.

考点:平行线分线段成比例定理
专题:选作题,立体几何
分析:要证四边形AECF是平行四边形,结合图形知BF是其一条对角线,故需连接另一条对角线AC,由四边形ABCD是平行四边形易知OA=OC,OC=OD,只要再证得OE=OF即可.
解答:
证明:连接A、C,设AC与BD交于点O.
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
又∵BE=DF,∴OE=OF.
∴四边形AECF是平行四边形.
∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
又∵BE=DF,∴OE=OF.
∴四边形AECF是平行四边形.
点评:本题考查了平行四边形的性质和证明,是一道基础题.熟练掌握性质定理和判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等比数列{an}的公比q<0,其前n 项的和为Sn,则a9S8与a8S9 的大小关系是( )
| A、a9S8>a8S9 |
| B、a9S8<a8S9 |
| C、a9S8≥a8S9 |
| D、a9S8≤a8S9 |
 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
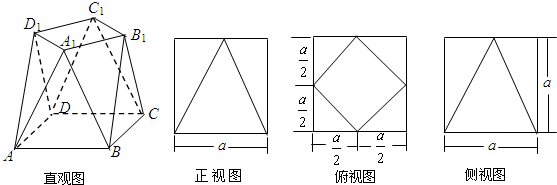
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):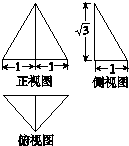 一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为
一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的表面积为