Question

多面体ABCD-A₁B₁C₁D₁的直观图，正视图，俯视图，侧视图如下所示．

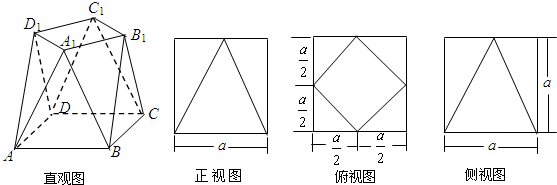
则此多面体的体积是

 

．

Answer 1

考点：由三视图求面积、体积

专题：计算题,空间位置关系与距离

分析：根据该多面体为长方体削去四个全等的三棱锥，先求出三棱锥的体积，然后利用长方体的体积减去四个全等的三棱锥的体积即可求出所求．

解答： 解：∵该多面体为长方体削去四个全等的三棱锥，
每个三棱锥的体积都为

1

3

×

1

2

×

a

2

×

a

2

×a=

1

24

a³．
∴此多面体的体积 V=a³-4•

1

24

a³=

5

6

a³．
故答案为：

5

6

a³．

点评：本题主要考查了多面体的体积，三棱锥的体积，确定多面体为长方体削去四个全等的三棱锥是关键，属于中档题．