题目内容
已知圆锥曲线
(θ为参数)和定点A(0,2),F1、F2是圆锥曲线的左右焦点,求经过点F1垂直于直线AF2的直线L的参数方程.
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:首先把参数方程转化成直角坐标方程,进一步求出椭圆的焦点坐标,再利用点斜式求出直线的方程,再把直线的直角坐标方程转化成参数方程.
解答:
解:圆锥曲线
(θ为参数)转化成直角坐标方程为:
+
=1
所以焦点坐标为:F1(-1,0)和F2(1,0)
则:KAF2=-2
所以:经过点F1垂直于直线AF2的直线L的方程为:y=-2x-2
所以转化为参数方程为:
(t为参数)
|
| x2 |
| 5 |
| y2 |
| 4 |
所以焦点坐标为:F1(-1,0)和F2(1,0)
则:KAF2=-2
所以:经过点F1垂直于直线AF2的直线L的方程为:y=-2x-2
所以转化为参数方程为:
|
点评:本题考查的知识要点:参数方程与直角坐标方程的相互互化,利用点斜式求直线的方程,属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为( )
如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为( )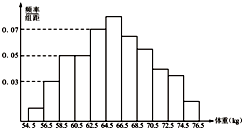 为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17.5岁到18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这200名学生中体重在[56.5,64.5]的学生人数是
为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17.5岁到18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这200名学生中体重在[56.5,64.5]的学生人数是