题目内容
已知抛物线y2=2px的准线与双曲线
-
=1(a>0)的两条渐近线分别交于M,N两点,O为坐标原点,△MON的面积为
,点P(x,y)为抛物线C上的动点,又点A(-1,0),F为抛物线的焦点,则
的最小值为 .
| x2 |
| a2 |
| y2 |
| 3a2 |
| 3 |
| |PF| |
| |PA| |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:双曲线
-
=1(a>0)的两条渐近线方程为y=±
x,抛物线y2=2px的准线x=-
,利用△MON的面积为
,求出抛物线的方程,
=
利用换元法,即可得出结论.
| x2 |
| a2 |
| y2 |
| 3a2 |
| 3 |
| p |
| 2 |
| 3 |
| |PF| |
| |PA| |
| |x+1| | ||
|
解答:
解:双曲线
-
=1(a>0)的两条渐近线方程为y=±
x,抛物线y2=2px的准线x=-
,
∵△MON的面积为
,
∴
•
p•
=
,
∴p=2,
∴y2=4x,
设P(x,y),则y2=4x,
∵定点A(-1,0),F(1,0),
∴
=
设t=
,x≥0,0<t≤1,
∴
=
,0<t≤1,
当t=
时,g(t)=-4t2+4t+1最大值为2,
∴
最小值为
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| 3a2 |
| 3 |
| p |
| 2 |
∵△MON的面积为
| 3 |
∴
| 1 |
| 2 |
| 3 |
| p |
| 2 |
| 3 |
∴p=2,
∴y2=4x,
设P(x,y),则y2=4x,
∵定点A(-1,0),F(1,0),
∴
| |PF| |
| |PA| |
| |x+1| | ||
|
设t=
| 1 |
| x+1 |
∴
| |PF| |
| |PA| |
| 1 | ||
|
当t=
| 1 |
| 2 |
∴
| 1 | ||
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查抛物线的方程,考查换元法,转化为二次函数的性质求解,属于中档题.

练习册系列答案
相关题目
已知全集U=R,A={x|x≤a+2},B={x|x≥a2},若∁U(A∩B)=R,则a的取值范围是( )
| A、[-1,2] |
| B、(-1,2) |
| C、(-∞,-1]∪[2,+∞) |
| D、(-∞,-1)∪(2,+∞) |
 如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为( )
如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
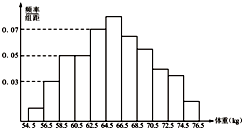 为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17.5岁到18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这200名学生中体重在[56.5,64.5]的学生人数是
为了了解某地区高三学生的身体发育情况,抽查了该地区200名年龄为17.5岁到18岁的男生体重(kg),得到频率分布直方图如图:根据如图可得这200名学生中体重在[56.5,64.5]的学生人数是