题目内容
已知凼数f(x)=x2-ax+2
(1)若f(x)>0解集为(-∞,1)∪(2,+∞),求a 的值;
(2)当x>0时,求
的最小值;
(3)若f (x)>1,解集为R,求实数a 的取值范围.
(1)若f(x)>0解集为(-∞,1)∪(2,+∞),求a 的值;
(2)当x>0时,求
| f(x) |
| x |
(3)若f (x)>1,解集为R,求实数a 的取值范围.
考点:二次函数的性质,一元二次不等式的解法
专题:函数的性质及应用
分析:(1)根据已知条件便知道方程x2-ax+2=0的两根为1,2,根据韦达定理即可求得a;
(2)求出
=x+
-a,由x>0,根据基本不等式即可得到
≥2
-a,所以便可求出
的最小值;
(3)根据已知条件容易得到x2-ax+1>0的解集为R,所以判别式△=a2-4<0,这样即可求得a的取值范围.
(2)求出
| f(x) |
| x |
| 2 |
| x |
| f(x) |
| x |
| 2 |
| f(x) |
| x |
(3)根据已知条件容易得到x2-ax+1>0的解集为R,所以判别式△=a2-4<0,这样即可求得a的取值范围.
解答:
解:(1)由题意得:1+2=a;
即a=3;
(2)
=x+
-a;
∵x>0,∴x+
≥2
,当x=
时取“=”;
∴
≥2
-a;
∴
的最小值为2
-a;
(3)由f(x)>1得:
x2-ax+1>0;
该不等式的解集为R;
∴△=a2-4<0;
∴-2<a<2;
∴实数a的取值范围为(-2,2).
即a=3;
(2)
| f(x) |
| x |
| 2 |
| x |
∵x>0,∴x+
| 2 |
| x |
| 2 |
| 2 |
∴
| f(x) |
| x |
| 2 |
∴
| f(x) |
| x |
| 2 |
(3)由f(x)>1得:
x2-ax+1>0;
该不等式的解集为R;
∴△=a2-4<0;
∴-2<a<2;
∴实数a的取值范围为(-2,2).
点评:考查一元二次不等式解和对应一元二次方程实数根的关系,韦达定理,基本不等式:a+b≥2
,a>0,b>0,以及一元二次不等式的解集为R时判别式△的取值情况.
| ab |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
平面向量的集合A 到A的映射f(
)=
-2(
•
)
,其中
为常向量.若映射f满足f(
)•f(
)=
•
对任意的
,
∈A恒成立,则
的坐标不可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A、(0,0) | ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(-
|
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线
-y2=1的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )
| x2 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
,
满足|
|=5,|
|≤1,且|
-4
|≤
,则
•
的最小值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| 21 |
| a |
| b |
A、
| ||||
| B、-5 | ||||
C、
| ||||
D、-
|
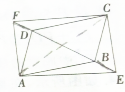
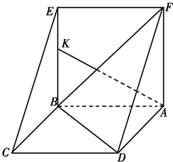 如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.
如图,边长为2的正方形ABCD绕AB边所在直线旋转一定的角度(小于180°)到ABEF的位置.