题目内容
已知二次函数f(x)=ax2+bx(a≠0)满足1≤f(-1)≤2,2≤f(1)≤4,则f(-2)的范围是( )
| A、[3,12] |
| B、(3,12) |
| C、(5,10) |
| D、[5,10] |
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意,1≤a-b≤2,2≤a+b≤4,f(-2)=4a-2b,转化为简单线性规划问题,从而求解.
解答:
解:∵二次函数f(x)=ax2+bx(a≠0)满足1≤f(-1)≤2,2≤f(1)≤4,
∴1≤a-b≤2,2≤a+b≤4,f(-2)=4a-2b,
作出其平面区域如下:

则由
解得,x=
,y=
;
即A(
,
);
同理,B(3,1);
则4×
-2×
≤f(-2)≤3×3-2×1,
即5≤f(-2)≤10,
故选D.
∴1≤a-b≤2,2≤a+b≤4,f(-2)=4a-2b,
作出其平面区域如下:

则由
|
| 3 |
| 2 |
| 1 |
| 2 |
即A(
| 3 |
| 2 |
| 1 |
| 2 |
同理,B(3,1);
则4×
| 3 |
| 2 |
| 1 |
| 2 |
即5≤f(-2)≤10,
故选D.
点评:本题考查了简单线性规划问题,要利用函数转化得到,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )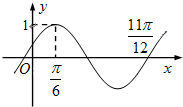
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
设α∈{-1,1,
,2,3},则使函数y=xα为奇函数α值的个数为( )
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
已知k∈[-2,1],则k的值使得过A(1,1)可以作两条直线与圆 x2+y2+kx-2y-
k=0相切的概率等于( )
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x-
在区间(1,+∞)上是增函数,则实数p的取值范围是( )
| p |
| x |
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,+∞) |
| D、[1,+∞) |