题目内容
已知抛物线C:y2=4x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若
=3
,则|QF|=( )
| FP |
| FQ |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求得直线PF的方程,与y2=4x联立可得x=1,利用|QF|=d可求.
解答:
解:设Q到l的距离为d,则|QF|=d,
∵
=3
,
∴|PQ|=2d,
∴直线PF的斜率为±
,
∵F(1,0),
∴直线PF的方程为y=±
(x-1),
与y2=4x联立可得x=
,
∴|
|=d=1+
=
.
故选:B.
∵
| FP |
| FQ |
∴|PQ|=2d,
∴直线PF的斜率为±
| 3 |
∵F(1,0),
∴直线PF的方程为y=±
| 3 |
与y2=4x联立可得x=
| 1 |
| 3 |
∴|
| QF |
| 1 |
| 3 |
| 4 |
| 3 |
故选:B.
点评:本题考查抛物线的简单性质,考查直线与抛物线的位置关系,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列命题中正确的是( )
| A、一直线与一平面平行,这个平面内有无数条直线与它平行 |
| B、平行于同一直线的两个平面平行 |
| C、与两相交平面的交线平行的直线必平行于这两个相交平面 |
| D、两条平行直线中的一条与一个平面平行,则另一条也与该平面平行 |
将直线2x-y+λ=0沿x轴向右平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
| A、-3或7 | B、-2或8 |
| C、0或10 | D、1或11 |
锐角△ABC中,角A,B,C所对的边分别为a,b,c,若C=2A,则
的取值范围是( )
| c |
| a |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
| D、(1,2) |
已知二次函数f(x)=ax2+bx(a≠0)满足1≤f(-1)≤2,2≤f(1)≤4,则f(-2)的范围是( )
| A、[3,12] |
| B、(3,12) |
| C、(5,10) |
| D、[5,10] |
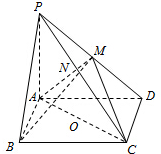 在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.
在四棱锥P-ABCD中,底面ABCD是矩形PA⊥ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M,交PC于点N.