题目内容

等差数列{an}中，若a1，a2013为方程x2-10x+16=0两根，则a2+a1007+a2012=（　　）
A、10B、15C、20D、40
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由方程的韦达定理求得a1+a2013，再由等差数列的性质求解．
解答： 解：∵a1，a2013为方程x2-10x+16=0的两根
∴a1+a2013=10
由等差数列的性质知：a1+a2013=a2+a2012=2a1007
∴a2+a1007+a2012=15
故选：B
点评：本题主要考查韦达定理和等差数列的性质，确定a1+a2013=10是关键．
练习册系列答案
相关题目
已知a，b都是区间[0，4]内任取的一个数，那么函数f（x）=
1
3
x3-ax2+b2x+2在x∈R上是增函数的概率是
 
．
在锐角△ABC中，角A，B，C所对的边分别为a，b，c．若a=2b，sinB=
3
4
，则（　　）
A、A=
π
3
B、A=
π
6
C、sinA=
3
3
D、sinA=
2
3
已知向量
a
=（cos
3x
2
，sin
3x
2
），
b
=（cos
x
2
，-sin
x
2
），且x∈[0，
π
2
]，若|
a
+
b
|=2
a
•
b
，则sin2x+tanx=（　　）
A、-1B、0C、2D、-2
cos42°•cos78°+sin42°•cos168°=
 
．
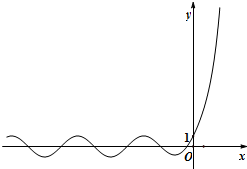已知函数：y=x2，y=log2x，y=2x，y=sinx，y=cosx，y=tanx．从中选出两个函数记为f（x）和g（x），若F（x）=f（x）+g（x）的图象如图所示，则F（x）=
 
．
已知函数f（x）=
x
，g（x）=
x
4x-a
．函数g（x）在（1，+∞）上单调递减．
（Ⅰ）求实数a的取值范围；
（Ⅱ）设函数h（x）=f（x）•g（x），x∈[1，4]，求函数y=h（x）的最小值．
已知函数f(x)=1-2sin2(x-
π
4
)，x∈R．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）判断函数f（x）在区间[-
π
6
，
π
6
]上是否为增函数？并说明理由．
已知双曲线
y2
a2
-
x2
b2
=1（a＞0，b＞0）的一条渐近线上有A，B两点，若直线l的方程为x+
2
y-2=0，且AB⊥l，则椭圆
x2
a2
+
y2
b2
=1的离心率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网