题目内容
已知a,b都是区间[0,4]内任取的一个数,那么函数f(x)=
x3-ax2+b2x+2在x∈R上是增函数的概率是 .
| 1 |
| 3 |
考点:几何概型
专题:概率与统计
分析:这是一个几何概型问题,我们可以先画出a,b∈[0,4],对应的平面区域的面积,然后再求出满足条件函数f(x)在R上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
解答:
 解:f'(x)=x2-2ax+b2
解:f'(x)=x2-2ax+b2
若函数f(x)在R上是增函数,则对于任意x∈R,f'(x)≥0恒成立.
所以,△=4a2-4b2≤0,即(a+b)(a-b)≤0
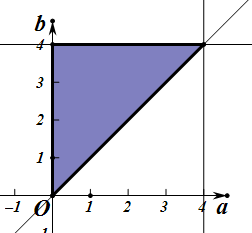
设“f(x)在R上是增函数”为事件A,则事件A对应的区域为{(a,b)|(a+b)(a-b)≤0}
全部试验结果构成的区域{Ω=(a,b)|0≤a≤4,0≤b≤4},如图.
所以函数f(x)在R上是增函数的概率是
=
.
故答案为:
 解:f'(x)=x2-2ax+b2
解:f'(x)=x2-2ax+b2若函数f(x)在R上是增函数,则对于任意x∈R,f'(x)≥0恒成立.
所以,△=4a2-4b2≤0,即(a+b)(a-b)≤0
设“f(x)在R上是增函数”为事件A,则事件A对应的区域为{(a,b)|(a+b)(a-b)≤0}
全部试验结果构成的区域{Ω=(a,b)|0≤a≤4,0≤b≤4},如图.
所以函数f(x)在R上是增函数的概率是
| ||
| 4×4 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:这是一个几何概型的概率题,本题的关键是找到事件对应的区域和试验的全部结果,根据几何概型公式就可以算出结果.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,有xf′(x)<f(-x)成立.(其中f′(x)是f(x)的导函数),若a=
f(
),b=f(1),c=log2
f(log2
)则a,b,c的大小关系是( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、a>b>c |
| B、c>b>a |
| C、b>a>c |
| D、c>a>b |
设x,y满足约束条件
,则z=x+2y的最大值是( )
|
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|
顶点在原点,经过圆C:x2+y2-2x+2
y=0的圆心且准线与x轴垂直的抛物线方程为( )
| 2 |
| A、y2=-2x | ||
| B、y2=2x | ||
C、y=
| ||
D、y=-
|
从数字1,2,3,4,5中,任意取出两个数字,不是连续的自然数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}中,若a1,a2013为方程x2-10x+16=0两根,则a2+a1007+a2012=( )
| A、10 | B、15 | C、20 | D、40 |
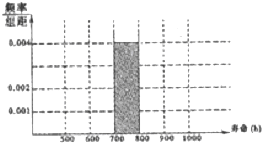 对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表:
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表: