题目内容
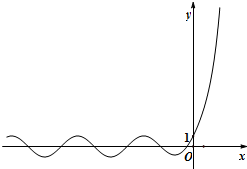 已知函数:y=x2,y=log2x,y=2x,y=sinx,y=cosx,y=tanx.从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=
已知函数:y=x2,y=log2x,y=2x,y=sinx,y=cosx,y=tanx.从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=考点:函数的图象
专题:函数的性质及应用
分析:观察图象可以得到,函数F(x)由图象可知,函数F(x)过定点(0,1),当x>0时,F(x)>1,为增函数,当x<0时,F(x)>0或,F(x)<0交替出现,
再思考所给的函数的图象和性质,即可得到答案
再思考所给的函数的图象和性质,即可得到答案
解答:
解:由图象可知,函数F(x)过定点(0,1),当x>0时,F(x)>1,为增函数,当x<0时,F(x)>0或,F(x)<0交替出现,
因为y=2x的图象经过点(0,1),且当当x>0时,y>1,当x<0时,0<y<1,
若为y=cosx,当x=0时,y=1,2x+cosx不满足过点(0,1),
所以只有当F(x)=2x+sinx才满足条件
故答案为:2x+sinx
因为y=2x的图象经过点(0,1),且当当x>0时,y>1,当x<0时,0<y<1,
若为y=cosx,当x=0时,y=1,2x+cosx不满足过点(0,1),
所以只有当F(x)=2x+sinx才满足条件
故答案为:2x+sinx
点评:本题考查了函数图象和识别,初等函数的图象和性质,属于基础题

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
顶点在原点,经过圆C:x2+y2-2x+2
y=0的圆心且准线与x轴垂直的抛物线方程为( )
| 2 |
| A、y2=-2x | ||
| B、y2=2x | ||
C、y=
| ||
D、y=-
|
等差数列{an}中,若a1,a2013为方程x2-10x+16=0两根,则a2+a1007+a2012=( )
| A、10 | B、15 | C、20 | D、40 |
条件p:
≥
,q:
,则p成立是q成立的( )
| a+b |
| 2 |
| ab |
|
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |
已知sinx+2cosx=0,则sin2x+1=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数
是纯虚数,则实数a的值为( )
| a-i |
| 1-2i |
| A、2 | ||
B、-
| ||
| C、-2 | ||
D、-
|