题目内容
4.在△ABC中,角A,B,C的对边分别是a,b,c已知c•cosB+(b-2a)cosC=0(1)求角C的大小
(2)若c=2,a+b=ab,求△ABC的面积.
分析 (1)利用正弦定理化简可得答案.
(2)根据(1)中C的大小,利用余弦定理求出ab的值可得△ABC的面积
解答 解:(1)∵c•cosB+(b-2a)cosC=0,
由正弦定理化简可得:sinCcosB+sinBcosC-2sinAcosC=0,即sinA=2sinAcosC,
∵0<A<π,
∴sinA≠0.
∴cosC=$\frac{1}{2}$.
∵0<C<π,
∴C=$\frac{π}{3}$.
(2)由(1)可知:C=$\frac{π}{3}$.
∵c=2,a+b=ab,即a2b2=a2+b2+2ab.
由余弦定理cosC=$\frac{1}{2}$=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
∴ab=(ab)2-2ab-c2.
可得:ab=4.
那么:△ABC的面积S=$\frac{1}{2}$absinC=$\sqrt{3}$.
点评 本题考查三角形的正余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
8.△ABC中,已知a=2,b=x,B=60°,如果△ABC 有两组解,则x的取值范围( )
| A. | x>2 | B. | $\sqrt{3}<$x<2 | C. | 2<x<$\frac{4}{3}$$\sqrt{3}$ | D. | 2<x≤$\frac{4}{3}$$\sqrt{3}$ |
9.曲线f(x)=-$\frac{\sqrt{3}}{3}{x}^{3}$+2在x=1处的切线倾斜角是( )
| A. | $\frac{1}{6}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{5}{6}π$ | D. | $\frac{2}{3}π$ |
14.设甲、乙两楼相距10m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是( )
| A. | $\frac{10\sqrt{3}}{3}$m,$\frac{40}{3}$$\sqrt{3}$ m | B. | 10$\sqrt{3}$ m,20$\sqrt{3}$ m | C. | 10($\sqrt{3}$-$\sqrt{2}$) m,20$\sqrt{3}$ m | D. | 10$\sqrt{3}$ m,$\frac{40}{3}$$\sqrt{3}$ m |
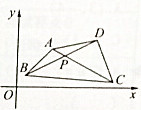 如图所示,已知A(4,5).B(1,2),C(12,1),D(11,6),求AC与BD的交点P的坐标.
如图所示,已知A(4,5).B(1,2),C(12,1),D(11,6),求AC与BD的交点P的坐标.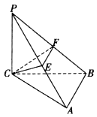 如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.
如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.