题目内容

12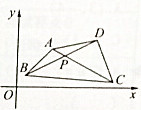．如图所示，已知A（4，5）．B（1，2），C（12，1），D（11，6），求AC与BD的交点P的坐标．

分析 利用点斜式可得直线AC，BD的方程，联立即可得出交点坐标．

解答 解：直线AC的方程为：y-1=$\frac{5-1}{4-12}$（x-12），化为：x+2y-14=0，
直线BD的方程为：y-2=$\frac{6-2}{11-1}$（x-1），化为：2x-5y+8=0，
联立$\left\{\begin{array}{l}{x+2y-14=0}\\{2x-5y+8=0}\end{array}\right.$，解得x=6，y=4．
∴P（6，4）．

点评 本题考查了直线的交点，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
16．函数f（x）=x3-3x-1，若对于区间[-3，2]上的任意x1，x2，都有|f（x1）-f（x2）|≤t，则实数t的最小值是20．
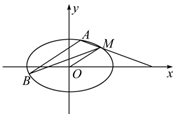17．如图，已知椭圆C的中心在原点，它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同，又椭圆C上有一点M（2，1），直线l平行于OM且与椭圆C交于A，B两点，连接MA，MB．
（1）求椭圆C的方程；
（2）求证：直线MA，MB与x轴所构成的三角形总是以x轴上所在线段为底边的等腰三角形．
14．已知抛物线C1：x2=4y的焦点F也是椭圆C2：$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$+=1（a＞b＞0）的一个焦点．C1与C2的公共弦长为2$\sqrt{6}$．
（Ⅰ）求C2的方程；
（Ⅱ）过点F的直线l与C1相交于A，B两点，与C2相交于C、D两点，且$\overrightarrow{AC}$，$\overrightarrow{BD}$同向．若|AC|=|BD|，求直线l的斜率．
7．如图所示的三棱柱ABC-A1B1C1中，底面是正三角形，侧棱BB1⊥面ABC，D是棱BC的中点，点M在棱BB1上，且CM⊥AC1．
（1）求证：A1B∥平面AC1D；
（2）求证：CM⊥C1D．
17．一个封闭立方体的六个面积各标出A，B，C，D，E，F这六个字母，现放成如图所示三种不同的位置，所看见的表面上的字母已标明，则字母A，B，C对面的字母分别是（　　）
A．D，E，FB．F，D，EC．E，F，DD．E，D，F
4．在△ABC中，角A，B，C的对边分别是a，b，c已知c•cosB+（b-2a）cosC=0
（1）求角C的大小
（2）若c=2，a+b=ab，求△ABC的面积．
1．已知函数f（x）=$\frac{{e}^{x}}{x}$-m（lnx+$\frac{1}{x}$）（m为实数，e=2.71828…是自然对数的底数）．
（Ⅰ）当m＞1时，讨论f（x）的单调性；
（Ⅱ）若g（x）=x2f′（x）-xex在（$\frac{3}{2}$，3）内有两个零点，求实数m的取值范围．
（Ⅲ）当m=1时，证明：xf（x）+xlnx+1＞x+$\frac{ln（x+1）}{x}$．
2．已知数列{an}是等差数列，a2=3，a6=7，则a11的值为（　　）
A．11B．12C．13D．10

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网