题目内容
8．△ABC中，已知a=2，b=x，B=60°，如果△ABC 有两组解，则x的取值范围（ ）| A． | x＞2 | B． | $\sqrt{3}＜$x＜2 | C． | 2＜x＜$\frac{4}{3}$$\sqrt{3}$ | D． | 2＜x≤$\frac{4}{3}$$\sqrt{3}$ |
分析 由△ABC 有两组解，可得2sin60°＜x＜2，解出即可得出．
解答 解：∵△ABC 有两组解，∴2sin60°＜x＜2，
解得$\sqrt{3}＜x＜2$．
故选：A．
点评 本题考查了正弦定理、解三角形，考查了推理能力与计算能力，属于中档题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
18．如图，已知$\overrightarrow{CA}=\overrightarrow a$，$\overrightarrow{CB}=\overrightarrow b$，AD=2DB，用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{DC}$为（ ）
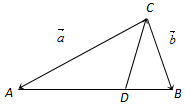
| A． | $\overrightarrow{DC}=-\frac{5}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | B． | $\overrightarrow{DC}$=$-\frac{1}{2}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C． | $\overrightarrow{DC}$=$-\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | D． | $\overrightarrow{DC}=-\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |
3．若cos α＞0，sin α＜0，则角 α的终边在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
20．用数列归纳法证明$\frac{1}{2}+cosα+cos2α+…+cosnα=\frac{{sin（n+\frac{1}{2}）α}}{{2sin\frac{α}{2}}}$时，验证n=1时，左边式子为（ ）
| A． | $\frac{1}{2}$ | B． | cosα | C． | $\frac{1}{2}+cosα$ | D． | $\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$ |
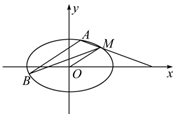如图，已知椭圆C的中心在原点，它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同，又椭圆C上有一点M（2，1），直线l平行于OM且与椭圆C交于A，B两点，连接MA，MB．