题目内容
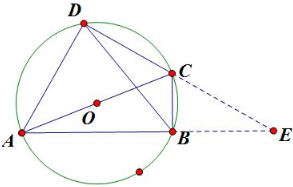
如图，四边形ABCD内接于圆O，∠BAD=60°，∠ABC=90°，BC=3，CD=5．求对角线BD、AC的长．
考点：与圆有关的比例线段
专题：直线与圆
分析：如图，延长DC，AB交于点E，由已知条件推导出∠ECB=60°，∠EBC=90°，∠E=30°，由此利用切割线定理、勾股定理和三角形相似能求出对角线BD、AC的长．
解答：
解：如图，延长DC，AB交于点E，
∵∠BAD=60°，∴∠ECB=60°，
∵∠ABC=90°，BC=3，CD=5，
∴∠EBC=90°，∴∠E=30°，
∴EC=2BC=2×3=6，
∴EB=
BC=3
，
∴ED=DC+EC=5+6=11，
∵EC×ED=EB×（EB+AB）
则6×11=3
×（3
+AB），
解得AB=
，
∴AC=
=
，
∵∠EDB=∠EAC，∠E=∠E，
∴△EDB∽△EAC，∴
=
，
∴BD=
=
=7．
∵∠BAD=60°，∴∠ECB=60°，
∵∠ABC=90°，BC=3，CD=5，
∴∠EBC=90°，∴∠E=30°，
∴EC=2BC=2×3=6，
∴EB=
| 3 |
| 3 |
∴ED=DC+EC=5+6=11，
∵EC×ED=EB×（EB+AB）
则6×11=3
| 3 |
| 3 |
解得AB=
13
| ||
| 3 |
∴AC=
32+(
|
14
| ||
| 3 |
∵∠EDB=∠EAC，∠E=∠E，
∴△EDB∽△EAC，∴
| BD |
| AC |
| BE |
| CE |
∴BD=
| AC•BE |
| CE |
| ||||||
| 6 |
点评：本题考查与圆有关的比例线段的求法，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
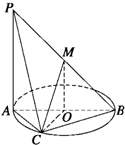如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：
如图，在平面直角坐标系xOy中，椭圆C：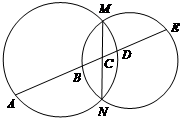
如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB•CD=BC•DE．