题目内容
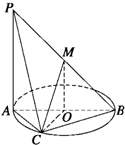如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：①PA∥平面MOB；②MO∥平面PAC；③OC⊥平面PAC；
④平面PAC⊥平面PBC．其中正确的命题是（ ）
| A、①和② | B、②和③ |
| C、③和④ | D、②和④ |
考点：命题的真假判断与应用,直线与平面平行的判定,直线与平面垂直的判定,平面与平面垂直的判定
专题：空间位置关系与距离
分析：①利用线面平行的判定定理即可判断出；
②利用三角形的中位线定理和线面平行的判定定理即可判断出；
③利用线面垂直的判定定理即可得出；
④利用圆的性质、线面面面垂直的判定与性质定理即可得出．
②利用三角形的中位线定理和线面平行的判定定理即可判断出；
③利用线面垂直的判定定理即可得出；
④利用圆的性质、线面面面垂直的判定与性质定理即可得出．
解答：
解：①∵PA?平面MOB，∴PA∥平面MOB不正确；
②由三角形的中位线定理可得MO∥PA，
又∵MO?平面PAC，PA?平面PAC，
∴MO∥平面PAC；
因此正确．
③∵OC与AC不垂直，因此OC⊥平面PAC不正确；
④∵PA⊥平面ABC，∴PA⊥BC．
由∠ACB是⊙O的直径AB所对的圆周角，
∴∠ACB=90°，即BC⊥AC．
又PA∩AC=A．
∴BC⊥平面PAC．
∴平面PAC⊥平面PBC．
因此④正确．
综上可知：其中正确的命题是②④．
故选：D．
②由三角形的中位线定理可得MO∥PA，
又∵MO?平面PAC，PA?平面PAC，
∴MO∥平面PAC；
因此正确．
③∵OC与AC不垂直，因此OC⊥平面PAC不正确；
④∵PA⊥平面ABC，∴PA⊥BC．
由∠ACB是⊙O的直径AB所对的圆周角，
∴∠ACB=90°，即BC⊥AC．
又PA∩AC=A．
∴BC⊥平面PAC．
∴平面PAC⊥平面PBC．
因此④正确．
综上可知：其中正确的命题是②④．
故选：D．
点评：本题综合考查了空间中线面面面的位置关系、圆的性质、三角形的中位线定理等基础知识与基本技能方法，属于基础题．
练习册系列答案
智慧小复习系列答案
相关题目
已知x，y满足
，且z=2x+y的最大值是最小值的4倍，则a的值是（ ）
|
A、
| ||
B、
| ||
C、
| ||
| D、4 |
