题目内容
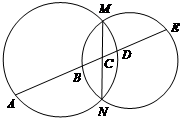如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB•CD=BC•DE．考点：与圆有关的比例线段
专题：直线与圆
分析：由A，M，D，N四点共圆，得到AC•CD=MC•CN；由M，B，N，E四点共圆，得到BC•CE=MC•CN，由此能够证明AB•CD=BC•DE．
解答：
解：∴A，M，D，N四点共圆，
所以AC•CD=MC•CN
∵M，B，N，E四点共圆，
∴BC•CE=MC•CN，
∴AC•CD=BC•CE，
即（AB+BC）•CD=BC•（CD+DE），
∴AB•CD=BC•DE．
所以AC•CD=MC•CN
∵M，B，N，E四点共圆，
∴BC•CE=MC•CN，
∴AC•CD=BC•CE，
即（AB+BC）•CD=BC•（CD+DE），
∴AB•CD=BC•DE．
点评：本题考查四点共圆的性质的应用，是中档题，解题时要认真审题，注意相交弦定理的合理运用．
练习册系列答案
相关题目
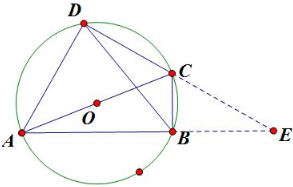
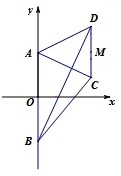如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，|AB|=
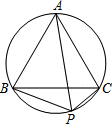如图，P是等边△ABC外接圆