题目内容
如图1,已知⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45°,∠DAB=60°,F为弧BC的中点.将⊙O沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
(Ⅰ)求证:OF∥AC;
(Ⅱ)在弧BD上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置;若不存在,请说明理由;
(Ⅲ)求二面角C-AD-B的正弦值.
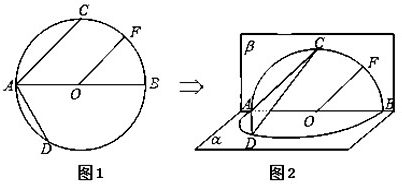
(Ⅰ)求证:OF∥AC;
(Ⅱ)在弧BD上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置;若不存在,请说明理由;
(Ⅲ)求二面角C-AD-B的正弦值.

考点:与二面角有关的立体几何综合题,直线与平面平行的性质
专题:空间向量及应用
分析:(Ⅰ)以O为坐标原点,以AB所在直线为y轴,以OC所在直线为z轴建立空间直角坐标系,求出向量
与
的坐标,利用向量共线的坐标表示求证OF∥AC,从而说明线面平行;.
(Ⅱ)假设在
上存在点G,使得FG∥平面ACD,根据(1)中的结论,利用两面平行的判定定理得到平面OFG∥平面ACD,从而得到OG∥AD,利用共线向量基本定理得到G的坐标(含有参数).
(Ⅲ)根据∠DAB=60°求出D点坐标,然后求出平面ACD的一个法向量,找出平面ADB的一个法向量,利用两平面法向量所成角的余弦值求解二面角C-AD-B的正弦值.
| AC |
| OF |
(Ⅱ)假设在
 |
| BD |
(Ⅲ)根据∠DAB=60°求出D点坐标,然后求出平面ACD的一个法向量,找出平面ADB的一个法向量,利用两平面法向量所成角的余弦值求解二面角C-AD-B的正弦值.
解答:
(Ⅰ)证明:如图,因为∠CAB=45°,连结OC,则OC⊥AB.
以AB所在的直线为y轴,以OC所在的直线为z轴,以O为原点,
作空间直角坐标系O-xyz,
则A(0,-2,0),C(0,0,2).

=(0,0,2)-(0,-2,0)=(0,2,2),
∵点F为
的中点,∴点F的坐标为(0,
,
),
=(0,
,
).
∴
=
,∴OF∥AC.
∵OF?平面ACD,AC?平面ACD,∴OF∥平面ACD.
(Ⅱ)解:设在
上存在点G,使得FG∥平面ACD,
∵OF∥平面ACD,∴平面OFG∥平面ACD,则有OG∥AD.
设
=λ
(λ>0),∵
=(
,1,0),
∴
=(
λ,λ,0).
又∵|
|=2,∴
=2,解得λ=±1(舍去-1).
∴
=(
,1,0),则G为
的中点.
∴在
上存在点G,使得FG∥平面ACD,且点G为
的中点.
(Ⅲ)解:∵∠DAB=60°,
∴点D的坐标D(
,1,0),
=(
,1,0).
设二面角C-AD-B的大小为θ,
设
=(x,y,z)为平面ACD的一个法向量.
由
,取x=1,解得y=-
,z=
.∴
=(1,-
,
).
取平面ADB的一个法向量
=(0,0,1),
∴cosθ=|cos<
,
>|=|
|=
.
∴sinθ=
=
=
.
∴二面角C-AD-B的正弦值为
.
以AB所在的直线为y轴,以OC所在的直线为z轴,以O为原点,
作空间直角坐标系O-xyz,
则A(0,-2,0),C(0,0,2).

| AC |
∵点F为
 |
| BC |
| 2 |
| 2 |
| OF |
| 2 |
| 2 |
∴
| OF |
| ||
| 2 |
| AC |
∵OF?平面ACD,AC?平面ACD,∴OF∥平面ACD.
(Ⅱ)解:设在
 |
| BD |
∵OF∥平面ACD,∴平面OFG∥平面ACD,则有OG∥AD.
设
| OG |
| AD |
| AD |
| 3 |
∴
| OG |
| 3 |
又∵|
| OG |
(
|
∴
| OG |
| 3 |
 |
| BD |
∴在
 |
| BD |
 |
| BD |
(Ⅲ)解:∵∠DAB=60°,
∴点D的坐标D(
| 3 |
| AD |
| 3 |
设二面角C-AD-B的大小为θ,
设
| n1 |
由
|
| 3 |
| 3 |
| n1 |
| 3 |
| 3 |
取平面ADB的一个法向量
| n2 |
∴cosθ=|cos<
| n1 |
| n2 |
| ||
1×
|
| ||
| 7 |
∴sinθ=
| 1-cos2θ |
1-(
|
2
| ||
| 7 |
∴二面角C-AD-B的正弦值为
2
| ||
| 7 |
点评:本题主要考查空间点、线、面位置关系,线面角、二面角及三角函数等基础知识,考查空间想象能力、运算能力和推理论证能力,考查用向量方法解决数学问题的能力.

练习册系列答案
相关题目
已知x,y满足
,且z=2x+y的最大值是最小值的4倍,则a的值是( )
|
A、
| ||
B、
| ||
C、
| ||
| D、4 |
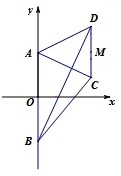 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=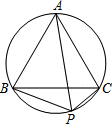 如图,P是等边△ABC外接圆
如图,P是等边△ABC外接圆